По определению арифметической прогрессией является последовательность чисел в которой каждый последующий член начиная со второго получается прибавлением к предыдущему некоторого числа
пусть исходная последовательность
a, a+d, a+2d,
что если к каждому члену этой прогрессии прибавить одно и тоже число b, то получится последовательность
a+b, a+d+b, a+2d+b,
a+b, (a+b)+d, (a+b)+d,
получилась последовательность в которой первый член равен a+b а каждый последующий получается прибавлением d что по определению является арифметической прогрессией
За властивістю геом. прогресії кожен член є середнім геометричним двох сусідніх членів:
Використаємо формулу :
Перший варіант нам підходить. Тоді матимемо стаціонарну арифметична прогресію 12, 12, 12, 12... Стаціонарна арифметична прогресія одночасно є стаціонарною геометричною прогресією.
Другий варіант:
До речі, перевіримо:
Бачимо, що та справді утворюють геометричну прогресію {12; 24; 48} зі знаменником 2.
Объяснение:
По определению арифметической прогрессией является последовательность чисел в которой каждый последующий член начиная со второго получается прибавлением к предыдущему некоторого числа
пусть исходная последовательность
a, a+d, a+2d,
что если к каждому члену этой прогрессии прибавить одно и тоже число b, то получится последовательность
a+b, a+d+b, a+2d+b,
a+b, (a+b)+d, (a+b)+d,
получилась последовательность в которой первый член равен a+b а каждый последующий получается прибавлением d что по определению является арифметической прогрессией
За властивістю геом. прогресії кожен член є середнім геометричним двох сусідніх членів:
Використаємо формулу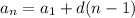
:
Перший варіант нам підходить. Тоді матимемо стаціонарну арифметична прогресію 12, 12, 12, 12... Стаціонарна арифметична прогресія одночасно є стаціонарною геометричною прогресією.
Другий варіант:
До речі, перевіримо:
Бачимо, що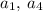
та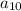 
справді утворюють геометричну прогресію {12; 24; 48} зі знаменником 2.
Відповідь. Умові задовольняють дві прогресії:
1) 12, 12, 12, 12, 12, 12.
2) 12, 16, 20, 24, 28, 32.