08 Застосування у колгоспі передової технологи дало можливість підвищити урожайність
картоплі з 1 га на 4 т. В результаті з ділянки площею 320 га зібрали на 640 т картоплі
більше, ніж раніше збирали з ділянки площею 400 га. Яка була врожайність картоплі
спочатку і якою вона стала?
1. Запишите выражение для Δy = f(х0 + Δх) − f(х) и найдите область определения функции Δу, если:
a) f(x) = arcsin x, х0 = 1/2; б) f(x) = arccos x, х0 = 0; в) f(x) = ln x, х0 = 2; г) f(x) = sin x, х0 = 2π.
2. Пользуясь определением производной, найдите производную функции: а) y = х в точке х = 1; б) y = х2 в точке х = х0;
в) y = в точке х = 4; г) y = х|х| в точке х = 0;
д) f(х) = (1 − cos x)/x при x ≠ 0,
0 при x = 0 в точке х = 0.
3. Функция y = f(х) имеет производную в точке а. Вычислите пределы последовательностей:
a) n(f(a + 1/n) − f/(a)); б) n(f(a) − f(a − 2/n));
в) n(f(a − 1/n) − f(a + 1/n));
г) n(f(a + 1/n) + f(a + 2/n) + … + f(a + k/n) − kf(a)).
4. Уравнения прямолинейного движения двух точек имеют вид: а) s1 = t, s2 = t2 (t ≥ 0); 6)
s1 = t2, s2 = t3 (t ≥ 0); в) s1 = ln t, s2 = (t ≥ 1) (t − время, s1 и s2 − расстояния, пройденные первой и второй точками за время t). Сравните мгновенные скорости этих двух точек, а также их средние скорости на отрезках времени 0 ≤ t ≤ 1 и 1 ≤ t ≤ 2 для случаев а) и б) и на отрезках 1 ≤ t ≤ 4 и 1 ≤ t ≤ 25 для случая в).
5. Составьте уравнение касательной к графику функции y = f(x) в точке с абсциссой x0, если:
а) f(x) = sin x, x0 = 0; б) f(x) = x2, x0 = 1;
в) f(x) = , x0 = 0; г) f(x) = arctg x, x0 = 1.
6. Найдите точку пересечения касательных к графику функции y = f(x) в точках с абсциссами x1 и x2, если:
а) f(x) = cos x, x1 = π/6, x2 = π/2; б) f(x) = ex, x1 = 0, x2 = 1; в) f(x) = arcsin x, x1 =0, x2 = 1/2.
Объяснение:
a) По условию составляем неравенство
-2x^2 + 2x -3 > -x -1
-2x^2 + 3x -2 > 0
2x^2 - 3x + 2 < 0
x^2 - 1.5x + 1 < 0
(x^2 - 0.75)^2 + 1 < 0 - не может быть ни при каких x, потому что значение выражения (x^2 - 0.75)^2 + 1 всегда положительно, значит, f(x) не будет больше g(x) ни при каких значениях x.
б) График функции y = f(x) находится ниже графика функции y =g(x), значит, выполняется неравенство f(x) < g(x)
x/3 < 6/x
x/3 - 6/x < 0
(x^2 - 18)/3x < 0
1.
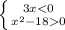3x < 0 ⇒ x<0 ⇒ x < -
(x +
)(x - 
) > 0 ⇒ x < -
или x>
2.
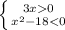3x > 0 ⇒ x>0
(x +
)(x - 
) < 0 ⇒ x < 
и x>-
⇒ 0<x < 
x < -
и 0<x < 