1.1. Теңдеудің дәрежесін анықтаңдар: 1) 4х6—2х7+x-1=0;
3) 4x4+xu-5x2+y=0;
5) xy+х2+2y=1;
7) (x-y)2+(x+y)2=22;
9) (22+x-y)3=x^узz4+1;
2) 52-у-2=0;
4) 8x+y+5x®y2=11;
6) xyz-x2-y2-22=2;
8) (x2+y2-ху)=xy”;
10) хуг?+x3–3xy2-22+9=0.
теңдеудің бос мүшесі жөнінде қорытынды жасаңдар.
1. Доказать тождество
sinα +sin5α+sin7α +sin11α = 4cos2α*cos3α*sin6α
sinα +sin5α+sin7α +sin11α =(sin5α +sinα) +(sin11α+sin7α) =
2sin3α*cos2α +2sin9α*cos2α =2cos2α*(sin9α+sin3α)=
2cos2α*2sin6α*cos3α =4cos2α*cos3α*sin6α
- - - - - - -
2.Найдите значение выражения sin2α*cos5α -sinα*cos6α ,если sinα = -1/√3
- - -
Cначала упростим выражение:
sin2α*cos5α -sinα*cos6α =2sinα*cos∝*cos5α - sinα*cos6α =
sinα(2cos5α*cos∝ - sinα*cos6α )=sinα*(cos6∝+cos4α -cos6α ) =
sinα*cos4α =sinα*(1 - 2sin²2α) = sinα*( 1 -2*(2sinα*cosα)² )=
= sinα*( 1 -8sin²α*cos²α ) =sinα*( 1 -8sin²α*(1 -sin²α) ) = || sinα =-1/√3 ||
= (-1/√3)*( 1 -8*(-1/√3)² *(1 - (-1/√3)² ) = - 1/√3 *( 1- (8/3)*(2/3) ) = 7√3 / 27
Если не учитывать, что 100% тоже больше 94%, то:
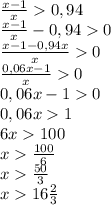
Пусть х - число домов в этом районе, а х-1 - число домов, имеющих больше 5 этажей
(чтобы найти минимально значение х, разница между числом домов, имеющих больше 5 этажей, и общим числом домов должна быть минимальна)
Получаем уравнение:
Проверка подбором
11 домов имеют больше 5 этажей
12 домов всего
11 / 12 = 0,91(6) = 91,(6)%
Не подходит.
...
15 домов имеют больше 5 этажей
16 домов всего
15 / 16 = 0,9375 = 93,75%
Не подходит.
16 домов имеют больше 5 этажей
17 домов всего
16 / 17 = 0,941176... = 94,1176...%
Подходит.
ответ: 17 - наименьшее число домов в данном районе.