0,404
Объяснение:
Пусть H₀ - вероятность отказа обеих микросхем.
Р(H₀)=0,07*0,1=0,007
Пусть Н₁ - вероятность отказа первой микросхемы при условии работо второй.
Вторая микросхема работает с вероятностью 1-0,1=0,9.
Р(Н₁)=0,07*0,9=0,063
Пусть Н₂ - вероятность отказа второй микросхемы при условии работо первой.
Первая микросхема работает с вероятностью 1-0,07=0,93.
Р(Н₂)=0,1*0,93=0,093.
Вероятность Н₃ работы обеих микросхем равна
P(Н₃)=0,9*0,93=0,837.
Вероятность отказа одной из микросхем (любой)
Р(Н₁)+Р(Н₂)=0,063+0,093=0,156.
Значит при условии отказа одной из микросхем (любой) это будет первая микросхема выражается отношением
Рассмотрим первый случай:
Если , то есть если или , то:
1) если и , то получаем верное равенство: , тогда — любое число;
2) если и , то получаем неверное равенство: , тогда уравнение не будет иметь решений;
3) если и , то получаем верное равенство: , тогда — любое число;
4) если и , то получаем неверное равенство: , тогда уравнение не будет иметь решений;
Рассмотрим второй случай:
Если , то есть если и , то
0,404
Объяснение:
Пусть H₀ - вероятность отказа обеих микросхем.
Р(H₀)=0,07*0,1=0,007
Пусть Н₁ - вероятность отказа первой микросхемы при условии работо второй.
Вторая микросхема работает с вероятностью 1-0,1=0,9.
Р(Н₁)=0,07*0,9=0,063
Пусть Н₂ - вероятность отказа второй микросхемы при условии работо первой.
Первая микросхема работает с вероятностью 1-0,07=0,93.
Р(Н₂)=0,1*0,93=0,093.
Вероятность Н₃ работы обеих микросхем равна
P(Н₃)=0,9*0,93=0,837.
Вероятность отказа одной из микросхем (любой)
Р(Н₁)+Р(Н₂)=0,063+0,093=0,156.
Значит при условии отказа одной из микросхем (любой) это будет первая микросхема выражается отношением
Рассмотрим первый случай:
Если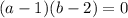 , то есть если
, то есть если 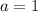 или
или 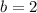 , то:
, то:
1) если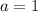 и
и 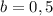 , то получаем верное равенство:
, то получаем верное равенство: 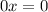 , тогда
, тогда  — любое число;
— любое число;
2) если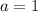 и
и 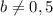 , то получаем неверное равенство:
, то получаем неверное равенство: 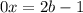 , тогда уравнение не будет иметь решений;
, тогда уравнение не будет иметь решений;
3) если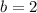 и
и 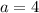 , то получаем верное равенство:
, то получаем верное равенство: 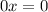 , тогда
, тогда  — любое число;
— любое число;
4) если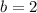 и
и 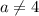 , то получаем неверное равенство:
, то получаем неверное равенство: 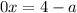 , тогда уравнение не будет иметь решений;
, тогда уравнение не будет иметь решений;
Рассмотрим второй случай:
Если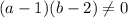 , то есть если
, то есть если 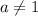 и
и 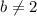 , то
, то 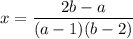
если