В решении.
Объяснение:
Если сторону квадрата уменьшить на 4 дм, то получится квадрат, площадь которого на 72 дм² меньше площади данного. Найдите исходную сторону квадрата.
х - исходная сторона квадрата.
х - 4 - уменьшенная сторона квадрата.
х² - площадь исходного квадрата.
(х - 4)² - площадь уменьшенного квадрата.
По условию задачи уравнение:
х² - (х - 4)² = 72
х² - (х² - 8х + 16) = 72
х² - х² + 8х - 16 = 72
8х = 72 + 16
8х = 88
х = 11 (дм) - исходная сторона квадрата.
Проверка:
11² - (11 - 4)² = 11² - 7² = 121 - 49 = 72 (дм)², верно.
Примем за 1 - объем цистерны
Пусть t цис./ч - производительность "медленного" насоса.
Тогда 3t цис./ч - производительность "быстрого" насоса.
(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.
(t+3t) - объем работы системы из двух насосов за 2ч 15мин.
Получим уравнение:
9t = 1
Значит, - цис./ч - производительность "медленного" насоса.
Тогда - цис./ч - производительность "быстрого" насоса.
Следовательно, ч - потребуется "быстрому" насосу на заполнение цистерны.
ответ: 3 ч.
В решении.
Объяснение:
Если сторону квадрата уменьшить на 4 дм, то получится квадрат, площадь которого на 72 дм² меньше площади данного. Найдите исходную сторону квадрата.
х - исходная сторона квадрата.
х - 4 - уменьшенная сторона квадрата.
х² - площадь исходного квадрата.
(х - 4)² - площадь уменьшенного квадрата.
По условию задачи уравнение:
х² - (х - 4)² = 72
х² - (х² - 8х + 16) = 72
х² - х² + 8х - 16 = 72
8х = 72 + 16
8х = 88
х = 11 (дм) - исходная сторона квадрата.
Проверка:
11² - (11 - 4)² = 11² - 7² = 121 - 49 = 72 (дм)², верно.
Примем за 1 - объем цистерны
Пусть t цис./ч - производительность "медленного" насоса.
Тогда 3t цис./ч - производительность "быстрого" насоса.
(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.
(t+3t)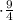 - объем работы системы из двух насосов за 2ч 15мин.
- объем работы системы из двух насосов за 2ч 15мин.
Получим уравнение: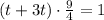
9t = 1
Значит,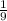 - цис./ч - производительность "медленного" насоса.
- цис./ч - производительность "медленного" насоса.
Тогда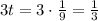 - цис./ч - производительность "быстрого" насоса.
- цис./ч - производительность "быстрого" насоса.
Следовательно,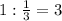 ч - потребуется "быстрому" насосу на заполнение цистерны.
ч - потребуется "быстрому" насосу на заполнение цистерны.
ответ: 3 ч.