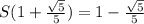Объяснение:
Для представления в виде многочлена стандартного вида выражения (а - с)(а + с) - (а - 2с)^2 мы начнем с выполнения открытия скобок.
Применим для этого формулу сокращенного умножения:
1. Квадрат разности:
(n - m)(n + m) = n^2 - m^2;
2. Квадрат разности:
(n - m)^2 = n^2 - 2nm + m^2.
Применим эти формулы и получаем:
(a - c)(a + c) - (a - 2c)^2 = a^2 - c^2 - (a^2 - 2 * a * 2c + 4c^2) = a^2 - c^2 - a^2 + 4ac - 4c^2.
Приводим подобные слагаемые:
a^2 - a^2 - c^2 - 4c^2 + 4ac = -5c^2 + 4ac.
ответ: -5c^2 + 4ac.
⊥
, так как
так как при любых х, D=225-240<0
- функция, зависящая от х.
Исследуем на наибольшее и наименьшее значение на
⇒
так как и возводя в квадрат получим:
Значит только одна точка возможного экстремума принадлежит данному отрезку [0,6;1,5]
Эта точка - точка минимума, так как при переходе через точку производная меняет знак с - на +
Значит наименьшее значение площади
Наибольшее значение на одном из концов отрезка:
при
- наибольшее значение
О т в е т. Наибольшее значение площади
наименьшее значение площади
Объяснение:
Для представления в виде многочлена стандартного вида выражения (а - с)(а + с) - (а - 2с)^2 мы начнем с выполнения открытия скобок.
Применим для этого формулу сокращенного умножения:
1. Квадрат разности:
(n - m)(n + m) = n^2 - m^2;
2. Квадрат разности:
(n - m)^2 = n^2 - 2nm + m^2.
Применим эти формулы и получаем:
(a - c)(a + c) - (a - 2c)^2 = a^2 - c^2 - (a^2 - 2 * a * 2c + 4c^2) = a^2 - c^2 - a^2 + 4ac - 4c^2.
Приводим подобные слагаемые:
a^2 - a^2 - c^2 - 4c^2 + 4ac = -5c^2 + 4ac.
ответ: -5c^2 + 4ac.
так как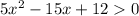
при любых х, D=225-240<0
Исследуем на наибольшее и наименьшее значение на![[0,6;1,5]](/tpl/images/1360/8622/d089f.png)
Значит только одна точка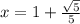
возможного экстремума принадлежит данному отрезку [0,6;1,5]
Эта точка - точка минимума, так как при переходе через точку производная меняет знак с - на +
Значит наименьшее значение площади
Наибольшее значение на одном из концов отрезка:
при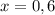
при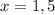
О т в е т. Наибольшее значение площади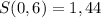
наименьшее значение площади