1/2x-x^2 - x-4/2x-x^2 =2/4-x^2​

^ - возведение в степень.

10-х^2=0

-x^2=-10

х^2=10

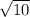х=+ и х=-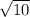

 

 

-х^2 - 8х=0

-х(х+8)=0

х=0 или (х+8)=0

             х=-8

ответ: 0, -8

 

 

х^2 + 36=0

х^2=-36 - неверное выражение (квардат числа не может быть равен отрицательному числу)

ответ:нет решений.

 

х^2 + 4х + 3=0

По теореме Виета находим корни:

х1+х2=-4

х1*х2=3

х1=-3 и х2=-1

ответ:-3, -1

 

х^2 +3х -28=0

Теорема Виета:

х1+х1=-3

х1*х2=-28

х1=-7 и х2=4

ответ: -7, 4

 

-5х^2 - 44х=0

-х(5х+44)=0

х=0 или 5х+44=0

            5х=-44

            х=-44/5=-8,8

ответ: -8,8, 0.

 

-х^2 - 10х-23=0

х^2+10х+23=0

Д=100-4*23=8

х1=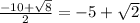

х2=

Итак, первый землекоп работал меньше на 1/3 часа. И его производительность меньше второго (так как если бы он копал один, то ему потребовалось бы на 1 час больше для завершения работы).
Имеем:
Пусть вся работа=1.
Производительность второго равна 1/Х.
Производительность первого равна 1/(Х+1).
Первый работал 1 час и произвел 1/(Х+1) работы.
Второй работал 4/3 часа и произвел 4/(3Х) работы.
вместе они сделали всю работу, то есть;
1/(Х+1)+4/(3Х)=1.
4Х+4+3Х=3Х²+3Х
3Х²-4Х-4=0
Х1=(2+√(4+12)/3=2
Х2=(2-4)/3 - корень отрицательный и нас не удовлетворяет.
Значит второй землекоп может в одиночку выполнить работу за 2 часа, а первый - за 3 часа.
Проверка: второй за 1/3 часа сделает (1/3)*(1/2)= 1/6 работы.
Затем вдвоем за 1 час они сделают 1*(1/2+1/3)=5/6 работы.
1/6+5/6=1. Они сделают всю работу за 1час 20минут.
ответ: первому на выполнение работы понадобится 3 часа, а второму 2 часа.