Мне кажется, что в условии задачи ошибка. Попытаюсь уточнить условие (дайте знать, правильно ли я понял):
Есть 4 карточки с надписями: делится на 7, простое, нечетное и больше 100. На другой стороне карточек написаны числа 2,5,7,12. Для любой карточки число, написанное на ней, не обладает свойством, написанным на ее обороте. Какое число написано на карточке с надписью делится на 7?
Записываем подходящих кандидатов для каждой карточки:
1) делится на 7: 2, 5, 12
2) простое: 12
3) нечетное: 2, 12
4) больше 100: 2, 5, 7, 12
Для 2-й карточки имеется единственный кандидат: 12. Следовательно, для 3-й карточки имеем: 3) нечетное: 2 (исключаем 12, записанное на 2-й карточке). На 1-й карточке остается число 5 (исключаем 2 и 12). На 4-й карточке остается число 7 (исключаем 2, 5 и 12, записанные на других карточках).
ответ: На обратной стороне карточки с надписью "делится на 7" написано число 5.
тут мы иммем дело с разницей квадрата под корнем. его надо уметь видеть.
= + 2ab +
= - 2ab +
в данном случе второе(минус перед два корней из семи).
И так 2√7 - в данном случае это у нас 2ab.
8 - это сума а в квадрате и б в квадрате.
то есть:
8 = +
2ab = 2√7
ab = √7
То есть нам нужно методом подбора подобрать такие числа, чтобы их сумма в квадрате была 8, а при умножении они давали корень из семи. (тут метод подбора ничего более просто нужны тренировки и практика для этого).
Я подобрала:
и 1. И в правду, * 1 =[/tex]\sqrt{7}[/tex]
и + = 7 + 1 = 8
то есть = = | - 1| (по модулю, модуль убираем, ибо |
Мне кажется, что в условии задачи ошибка. Попытаюсь уточнить условие (дайте знать, правильно ли я понял):
Есть 4 карточки с надписями: делится на 7, простое, нечетное и больше 100. На другой стороне карточек написаны числа 2,5,7,12. Для любой карточки число, написанное на ней, не обладает свойством, написанным на ее обороте. Какое число написано на карточке с надписью делится на 7?
Записываем подходящих кандидатов для каждой карточки:
1) делится на 7: 2, 5, 12
2) простое: 12
3) нечетное: 2, 12
4) больше 100: 2, 5, 7, 12
Для 2-й карточки имеется единственный кандидат: 12. Следовательно, для 3-й карточки имеем: 3) нечетное: 2 (исключаем 12, записанное на 2-й карточке). На 1-й карточке остается число 5 (исключаем 2 и 12). На 4-й карточке остается число 7 (исключаем 2, 5 и 12, записанные на других карточках).
ответ: На обратной стороне карточки с надписью "делится на 7" написано число 5.
тут мы иммем дело с разницей квадрата под корнем. его надо уметь видеть.
в данном случе второе(минус перед два корней из семи).
И так 2√7 - в данном случае это у нас 2ab.
8 - это сума а в квадрате и б в квадрате.
то есть:
8 =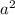 +
+ 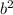
2ab = 2√7
ab = √7
То есть нам нужно методом подбора подобрать такие числа, чтобы их сумма в квадрате была 8, а при умножении они давали корень из семи. (тут метод подбора ничего более просто нужны тренировки и практика для этого).
Я подобрала:
и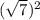 +
+ 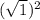 = 7 + 1 = 8
= 7 + 1 = 8
то есть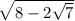 =
= 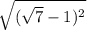 = |
= |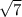 - 1| (по модулю, модуль убираем, ибо
- 1| (по модулю, модуль убираем, ибо 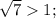 |
|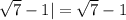
То есть:
ответ: -1.