1) автомобиль, пройдя путь от а до в, равный 300 км, повернул назад, увеличив скорость на 12 км/ч. в результате на обратный путь он затратил на 50 мин меньше, чем на путь от а до в. найдите первоначальную скорость
автомобиля. ( решите, выделяя все три этапа) 2) докажите, что не существует такого значения k, при котором уравнение х²-2kх+к-3=0 имело бы только один корень. 3)пусть х1 и х2- корни уравнения 2х²-9х-12=0 а) х1²х2+х1х2² б) х2/x1+x1/x2 в
х1 в кубе+ х2 в кубе
Пусть первоначальная скорость равна х км/ч, а после увеличения скорости - (x+12) км/ч. Время пути из пункта А в пункт В, равно 300/х ч, а из пункта В в пункт А - 300/(x+12) ч. На обратный путь автомобиль затратил на 50 мин меньше, чем на путь от А до В, значит составляем и решим уравнение
50 мин = 50/60 ч = 5/6 ч.
По теореме Виета
ответ: 60 км/ч.
2) Найдем дискриминант квадратного уравнения
D>0 для всех действительных k имеет два действительных корня, значит нет такого значения k в котором квадратное уравнение имело бы только один корень.
3) Квадратное уравнение имеет корни(т.к.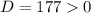 ), значит можем воспользоваться теоремой Виета.
), значит можем воспользоваться теоремой Виета.