1. Чертёж детали, без применения компьютерной техники, всегда выполняется: а) без применения чертёжных инструментов; б) только с применением чертёжных инструментов; в) без соблюдения масштаба; г) с точным соблюдением масштаба
1. Прежде всего, разобьем это выражение на множители:
n^4+2n^3+3n^2+2n=n*(n^3+2n^2+3*n+2)
Разделив столбиком многочлен n^3+2n^2+3*n+2 на (n+1), получаем (n^2+n+2). Т.е. исходный многочлен может быть представлен в следующем виде:
n^4+2n^3+3n^2+2n=n*(n+1)*(n^2+n+2)
2. Теперь рассмотрим 2 случая:
а). Пусть n - четное число, т.е. делится на 2 без остатка, тогда
n делится на 2 без остатка;
(n+1), будучи числом нечетным, не делится на 2 без остатка;
Теперь рассмотрим n^2+n+2:
n - четное, значит n^2 - тоже четное, и n^2+n - тоже четное, т.е. делится на 2 без остатка. Т.к. n^2+n уже делится на 2 без остатка, то n^2+n+2 также еще раз разделится на 2 без остатка => (n^2+n+2)/2=((n^2+n)/2) + 2/2=((n^2+n)/2)+1.
Получаем, что исходное выражение можно три раза разделить на 2, т.е. разделить на 8.
б). Пусть n - нечетное, т.е. не делится на 2 без остатка, тогда
n не делится на 2 без остатка;
(n+1), будучи числом четным, делится на 2 без остатка;
n - нечетное, значит n^2 - тоже нечетное, а n^2+n - уже четное, т.к. к нечетному n^2 прибавляем нечетное n. И аналогично, т.к. n^2+n уже делится на 2 без остатка, то n^2+n+2 также еще раз разделится на 2 без остатка.
Получаем, что исходное выражение можно три раза разделить на 2, т.е. разделить на 8.
1. Прежде всего, разобьем это выражение на множители:
n^4+2n^3+3n^2+2n=n*(n^3+2n^2+3*n+2)
Разделив столбиком многочлен n^3+2n^2+3*n+2 на (n+1), получаем (n^2+n+2). Т.е. исходный многочлен может быть представлен в следующем виде:
n^4+2n^3+3n^2+2n=n*(n+1)*(n^2+n+2)
2. Теперь рассмотрим 2 случая:
а). Пусть n - четное число, т.е. делится на 2 без остатка, тогда
n делится на 2 без остатка;
(n+1), будучи числом нечетным, не делится на 2 без остатка;
Теперь рассмотрим n^2+n+2:
n - четное, значит n^2 - тоже четное, и n^2+n - тоже четное, т.е. делится на 2 без остатка. Т.к. n^2+n уже делится на 2 без остатка, то n^2+n+2 также еще раз разделится на 2 без остатка => (n^2+n+2)/2=((n^2+n)/2) + 2/2=((n^2+n)/2)+1.
Получаем, что исходное выражение можно три раза разделить на 2, т.е. разделить на 8.
б). Пусть n - нечетное, т.е. не делится на 2 без остатка, тогда
n не делится на 2 без остатка;
(n+1), будучи числом четным, делится на 2 без остатка;
n - нечетное, значит n^2 - тоже нечетное, а n^2+n - уже четное, т.к. к нечетному n^2 прибавляем нечетное n. И аналогично, т.к. n^2+n уже делится на 2 без остатка, то n^2+n+2 также еще раз разделится на 2 без остатка.
Получаем, что исходное выражение можно три раза разделить на 2, т.е. разделить на 8.
1) проверяем условие при наименьшем возможном значении n.
n>5, значит проверяем условие при n=6
Верно!
2) Сделаем предположение, что для всех n=k, k>5 верно неравенство:
3) Тогда при n=k+1 должно выполняться неравенство:
Вернемся к неравенству из второго пункта и домножим его на 2:
Подставим 2k² в 3-й пункт и рассмотрим полученное неравенство:
по методу интервалов определяем, что неравенство k²-2k-1>0 выполняется при k>1+√2, тогда при k>5 оно тоже выполняется (так как 5>1+√2)
Тогда обратным ходом получаем 2k²>k²+2k+1 при k>5 или 2k²>(k+1)² при k>5
Если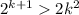
, а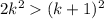 
, при k>5
То есть,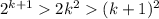
, при k>5, то по закону транзитивности: