1) Что называется периодом функции? 2) Как различить периодичность функции по графику?
3) Как определить период функции по графику?
4) Может ли функция иметь два различных периода?
5) Какой из периодов принимается как основной?
6) Приведите пример четной периодической функции.
7) Приведите пример нечетной периодической функции.
8) Как не пользуясь графиком можно определить период функций
заданной формулой?
до
Давай я попробую тебе сначала объяснить как делать Б,
Чтобы решать такие задания, тебе необходимо знать формулы сокращённого умножения, и формулу нахождения дискриминанта.
1) (a + b)² = a² + 2ab + b²
2) (a – b)² = a² – 2ab + b²
3 ) (a + b)(a – b) = a² – b²
А теперь перейдем к примеру:
и видим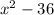
это ни что иное, как формула под номером 3 (разность квадратов, расписываем ее (х-6)(х+6)
Все мы знаем, что при делении 1 дроби на 2, необходимо вторую перевернуть, так мы переходим к умножению
2х+2 тут тоже все просто , выносим 2 за скобку , и получаем 2*(х+1)
осталось перейти к самому сложно, и кстати если вы заметили
Когда видишь что-то похожее на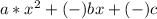
, где а, b,c цифры, значит тебе нужно искать дискриминант.
Д= b² -4 a c = 25-4*1*(-6) = 49= 7²
x₁=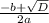
=( 5+7)/2 = 6
x₂ =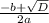
= (5-7)/2= -1
это все записывается потом так (х-6) (х+1) ( тоже формула)
наше уравнение теперь выглядит так:
ответ: x+6
теперь перейдем к уравнению А, учитывая, что мы почти его сделали.
Д= b² -4 a c = 25-4*1*(-6) = 49= 7²
x₁=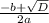
=( 5+7)/2 = 6
x₂ =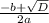
= (5-7)/2= -1
(х-6) (х+1)=0
Допустимые значения:
x-6=0 x+1=0
x=6 x=-1
ответ: (- ∞; - 1] ; [-1;6]; [6; +∞)
В решении.
Объяснение:
Побудуйте графік функції y=x²-4x-5. Користуючись графіком, знайдіть:
1) Найменше значення функції;
2) Множину розв'язків нерівності x²-4x-5>0;
3) Проміжок, на якому функція y=x²-4x-5 зростає.
Постройте график функции y = x² - 4x - 5.
Пользуясь графиком, найдите:
1) Наименьшее значение функции;
2) Множество решений неравенства x²- 4x - 5 > 0;
3) Промежуток, на котором функция y = x² - 4x - 5 возрастает.
Придать значения х, подставить в уравнение, вычислить значения у, записать в таблицу, построить по точкам график.
График квадратичной функции, парабола со смещённым центром, ветви направлены вверх.
Таблица:
х -2 -1 0 1 2 3 4 5 6
у 7 0 -5 -8 -9 -8 -5 0 7
1) Наименьшее значение функции определяется ординатой её вершины. Согласно графика, наименьшее значение у = -9.
2) x²- 4x - 5 > 0;
Приравнять к нулю:
x²- 4x - 5 = 0
Уравнение квадратичной функции, ветви направлены вверх, пересекают ось Ох при х = -1 и х = 5.
Решение неравенства: х∈(-∞; -1)∪(5; +∞).
Неравенство строгое, скобки круглые.
3) Функция возрастает при х∈(2; +∞).
На промежутке от х = 2 до + бесконечности.