1. дана функция y(x)=x-1/x+2. найдите произведение значений функции y(-1)*y(2)*y(3). 2. для функции y = 2+3*(2x+1)²+7|4x+2| найдите значения у(-3/2) и у(1/2) и сравните их.
y=x²-4x-5 проверка по Виету корни 5 и -1. График строить по точкам обоих корней, вершины х=2 y=-9 и пересечения с осью у х=0 у=-5 ось симметрии х=2
3. |x-3|=-√x+3 аналитически 0<x<3 3-x=-√x+3 видим корень х=0 x-3=-√x+3 x+√x=6 x²+x²+2x√x=36 x²+x√x=36 √x=t t⁴+t³=36 и так далее... Но нас просят решить графически. Строим |x-3| это "галочка сидящая на х=3". мы строим 2 луча из точки х=3 по формулам у=х-3 при х≥3 у=3-х при х<3. Затем строим у=-√х +3 или непонятно -√(х+3) График строится по точкам - под корнем≥0 в первом случае х≥0 в другом х≥-3 и ищутся точки пересечения двух графиков.
104.
a) cos 120 =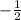
б) sin(-150)= -sin 150=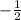
в) tg(-225)= -tg 225 = -1
г) cos(-225)=cos 225=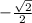
д) cos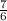
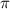 = cos 630 = 0
= cos 630 = 0
е)sin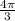 = sin 240 =
= sin 240 =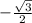
106.
а) sin ( -
-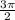 ) = sin (
) = sin ( -270) = sin (270-
-270) = sin (270- ) = -cos
) = -cos 
б) cos ( -
-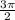 )= cos (
)= cos ( -270) = cos (270-
-270) = cos (270- ) = -sin
) = -sin 
в) tg ( -2
-2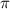 ) = tg (
) = tg ( -360) = tg (360-
-360) = tg (360- ) = -tg
) = -tg 
Объяснение:
104.
cos(-α)= cos α
sin(-α)= -sin α
tg(-α)= -tg α
ctg(-α)= -ctg α
a) cos 120 =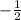
б) sin(-150)= -sin 150=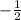 ( т.к. sin непарная функция => sin(-α)= -sin α )
( т.к. sin непарная функция => sin(-α)= -sin α )
в) tg(-225)= -tg 225 = -1 ( т.к. tg непарная функция => tg(-α)= -tg α )
г) cos(-225)=cos 225=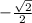 ( т.к. cos парная функция => cos(-α)= cos α )
( т.к. cos парная функция => cos(-α)= cos α )
д) cos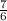
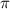 =
= 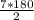 =630, 630=360+270 ( 360 это один полный оборот)
=630, 630=360+270 ( 360 это один полный оборот)
=> cos 270 cos 270 = 0
е)sin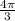 = sin 240 =
= sin 240 =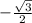
106.
В этом номере я использовал формулы приведения
их можно найти в интернете
а) sin ( -
-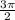 ) = sin (
) = sin ( -270) = sin (270-
-270) = sin (270- ) = -cos
) = -cos 
б) cos ( -
-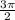 )= cos (
)= cos ( -270) = cos (270-
-270) = cos (270- ) = -sin
) = -sin 
в) tg ( -2
-2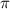 ) = tg (
) = tg ( -360) = tg (360-
-360) = tg (360- ) = -tg
) = -tg 
2. y=ax²+bx+c y(5)=0 y(-1)=0
25a+5b+c=0 a-b+c=0
x0 вершины = (5-1)/2=2 4a+2b+c=-9
b=a+c 4a+2a+2c+c=6a+3c=-9 или 2a+c=-3 c=-3-2a
25a+5(a-3-2a)-3-2a=0 25a+5a-15-10a-3-2a=0
18a=15+3=18 a=1 c=-3-2a=-3-2=-5 b=a+c=1-5=-4
y=x²-4x-5 проверка по Виету корни 5 и -1. График строить по точкам обоих корней, вершины х=2 y=-9 и пересечения с осью у
х=0 у=-5 ось симметрии х=2
3. |x-3|=-√x+3 аналитически 0<x<3 3-x=-√x+3 видим корень х=0
x-3=-√x+3 x+√x=6 x²+x²+2x√x=36 x²+x√x=36 √x=t t⁴+t³=36 и так далее... Но нас просят решить графически. Строим |x-3| это "галочка сидящая на х=3". мы строим 2 луча из точки х=3 по формулам у=х-3 при х≥3 у=3-х при х<3. Затем строим у=-√х +3 или непонятно -√(х+3) График строится по точкам - под корнем≥0 в первом случае х≥0 в другом х≥-3 и ищутся точки пересечения двух графиков.