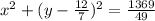1. даны векторы a={4; -2,-4}, b={6; -3; 2}. вычислить: (2a-3b)(a+2b)
2. даны вершины треугольника a (3; 2; -3), b(5; 1; -1), c(1; -2; 1). определить его внешний угол при вершине а.

Примем

S=12, км - путь туристов туда и обратно;

V1, км/час - скорость лодки (скорость в стоячей воде);

V2=3 км/час - скорость течения

тогда

S/(V1+V2)+S/(V1-V2)=3

12/(V1+3)+12/(V1-3)=3

[12*(V1-3)+12*(V1+3)]-3*(V1+3)*(V1-3)=0

12*V1-36+12*V1+36-3*(V1^2-3*V1+3*V1-9)=0

12*V1+12*V1-3*V1^2+27=0

-3*V1^2+24*V1+27=0

Решаем при дискриминанта (см. ссылку)

V1(1)=9

V1(2)=-1

скорость не может быть отрицательная

тогда

скорость лодки в стоячей воде = 9 км/час

проверим

12/(9+3)+12/(9-3)=3

12/12+12/6=3

1+2=3

3=3

Решение верно.

Пусть точка C(0, m) - центр окружности (так как по условию центр лежит на оси OY, то первая координата равна 0)

Известно, что расстояние от центра до любой точки на окружности является константой и равно радиусу R окружности

Наша окружность проходит через точку 7 на оси OY, значит R = 7 - m

Также окружность проходит через точку 5 на оси OX, значит по теореме Пифагора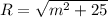

Приравняем это и получим уравнение:

Возвёдём в квадрат и решим уравнение:

Координата центра окружности  -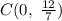  

Радиус окружности: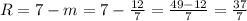

Уравнение окружности выглядит следующим:

Подставим наши числа:

ответ: