1) Егер арифметикалық прогрессияның бірінші және төртінші мүшелерінің қосындысының мәні 23-ке, үшінші және алтыншы
мүшелерінің қосындысының мәні 31-ге тең болса, онда оның бірінші
мүшесі мен айырымын табыңдар.
2) Егер геометриялық прогрессияның бірінші және үшінші мүше-
лерінің қосындысының мәні 49,2-ге, бірінші және үшінші мүше-
лерінің айырымының мәні -15,6-ға тең болса, онда оның бірінші
мүшесі мен еселігін табыңдар.
3) а2+а4 =3,4 болса, онда арифметикалық прогрессияның алғашқы
бес мүшесінің қосындысының мәнін табыңдар.
2 2 180 х 4 равняется 720
Объяснение:
тактак как в треугольнике если провести диагональ получается четыре треугольника то треугольника в треугольнике общая сумма 180 градусов сначала 180 умножать на число квадратов получивший 4 получается 180 на 4 равно 720по формуле формула такая скобка открывается икс минус 2 скобка закрывается x 180 - это количество углов то есть у нас в данном случае 8 не являются соседями являются значит 8 - 2получается 6 если сделать по диагонали это получается треугольники значит 180 так задание получается 1080 градусовукажи номеров и полках треугольника это получается 1 и 4 если разделить провести прямую то она остается в своей фигурами значит это выпуклыйсамый последний 5 найти в 12 см каждая сторона 12 значит 12 + 4 раза + 13 + 12 + 12 + 12 ещё плюс 12 получилось 4 раза 12 24 36 48 получается 48 см ну всё
A) х>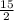
Б)0>x
Объяснение:
а) 9x+15<3(7x-5) "Идет метод фонтанчика умножаем 3 на 7x минус 3 умножить на 5"
9x+15<3*7x-3*5
9x+15<21x-15 "Дальше можно сократить цифры находящиеся перед X"
9 и 21 - Общий множитель 3 "Делим их на 3"
3 и 7 - убираем обратно
3х+15<7х-15 "ДАЛЬШЕ ПЕРЕНОСИМ иксы к иксам числа к числам
3x-7x<-15-15
-4x<-30
x=30/-4
х>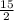
б) 5(4x-2)>11x-10 "Идет метод фонтанчика умножаем 5 на 4x минус 5 умножить на 2"
20x-10>11x-10 "Дальше нужно убрать -10 потому что он и там и там одинаковый"
20x>11x
x>0
Удачи в учёбе