1°. Функцію задано формулою у=-х+6. Визначте: 1) значення функції, якщо значення аргументу дорівнює 5; 2) значення аргументу, при якому значення функції дорівнює –8; 3) чи проходить графік функції через точку А(-3;9).

Показать ответ

Ответ:

Матрос573

29.12.2020 05:43

1. область определения х принадлежит (-бесконечность;+бесконечность).

2. пересечение с осью ординат (ОУ): x=0 f(x)=-1

3. исследование функции на четность/нечетность:

f(x)=x^3-2x^2+x-1

f(-x)=-x^3-2x^2-x-1 функция не является ни четной ни нечетной

4. производная функции:

3х^2-4x+1/

нули производной:

х=1/3. х=1.

5. Функция возрастает. х принадлежит (-беск.;1/3] U [1/3;+беск).

функция убывает. х принадлежит [1/3;1]

6. минимальное значение функции. -бесконечность

максимальное значение функции +бесконечность

0,0(0 оценок)

Ответ:

alkadraz12321

08.02.2020 20:20

1)2x³-x³+7x2+x-4x²-5х=2x³-x³+14+x-4x²-5x=x³+14-4x-4x²=x³-4x²-4x+14 при х=2

2³-4*2²-4*2+14=8-2⁴-8+14=8-16-8+14=-2

2) 0,46³ -0,26² +0,56 -0,363-0,56+7=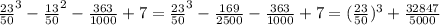 $\frac{23}{50}^3-\frac{13}{50}^2-\frac{363}{1000}+7=\frac{23}{50}^3-\frac{169}{2500}-\frac{363}{1000}+7=(\frac{23}{50})^3+\frac{32847}{5000}$ ≈6.666736

3) -4a²b+3ab2 +3a²b-5ab2+5а²b=4a²b+3ab2-5ab2=4a²b-2ab2=4a²b-4ab=4ab(a-1) при а=5 b=-0.4=4*5*(-0.4)(5-1)=4*5(-0.4)*4=-32

4) -0,3x-13xy2-37ху²=-0,3x-(13*2)xy-37xy²=-0,3x-26xy-37xy² при х=4 у=-0,2 =-0,3*4-26*4*(-0,2)-37*4*(-0,2)²=4(-0,3+26*0,2-37*(-0,2)²)=4(-0,3+5,2-37*0,2²)=4(-0,3+5,2-37*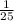 $\frac{1}{25}$ )=4(-0,3+5,2- $\frac{37}{25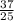}$ )=4(-0,3+5,2-1,48)=4*3,42=13,68