1) Из каждой вершины выпуклого многогранника исходит три рёбра. Сколько вершин и граней имеет этот многогранник, если число его рёбер равно a)12; b)15 2)Из каждой вершины выпуклого многогранника исходит четыре рёбра. Сколько вершин и граней имеет этот многогранник, если число его рёбер равно 12
x^2+3x-5=0 - это биквадратное уравнение, соответствующее формуле ax^2+bx+c=0, где a,b,c - числа
Уравнение дискриминанта: D=a^2-4ac (если оно меньше 0, то у уравнения нет корней, если больше нуля, то 2 корня, если меньше - 1)
x=(-b+-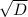 ) / 2a из-за +- и есть x1 и x2
) / 2a из-за +- и есть x1 и x2
Решаем:
a=1; b=3; c=-5;
D= 1-4*1*(-5)= 21 >0 значит у уравнения 2 корня
x1=-3(1+![\sqrt[2]{3}](/tpl/images/1363/0237/30a2c.png) )/2
)/2
x2=-3(1-![\sqrt[2]{3}](/tpl/images/1363/0237/30a2c.png) )/2
)/2
переворачиваем дробь(т.к. у нас деление на 1): 2/-3(1+![\sqrt[2]{3}](/tpl/images/1363/0237/30a2c.png) ) и с x2 делаем тоже самое
) и с x2 делаем тоже самое
поучаем выражение 2/-3(1+![\sqrt[2]{3}](/tpl/images/1363/0237/30a2c.png) )+2/-3(1-
)+2/-3(1-![\sqrt[2]{3}](/tpl/images/1363/0237/30a2c.png) ) домножаем на выражения в скобках и складываем дроби: (2(1-
) домножаем на выражения в скобках и складываем дроби: (2(1-![\sqrt[2]{3}](/tpl/images/1363/0237/30a2c.png) )+2(1+
)+2(1+![\sqrt[2]{3}](/tpl/images/1363/0237/30a2c.png) ))/-3(1-
))/-3(1-![\sqrt[2]{3}](/tpl/images/1363/0237/30a2c.png) )(1+
)(1+![\sqrt[2]{3}](/tpl/images/1363/0237/30a2c.png) ) = 4/-3(1^2-
) = 4/-3(1^2-![\sqrt[2]{3}](/tpl/images/1363/0237/30a2c.png) ^2)=4/6=2/3
^2)=4/6=2/3