См объяснение
Объяснение:
а) так как перед стоит положительный коэффициент (равный единице), следовательно ветви параболы направлены вверх
б) координаты вершины (x0, y0) вычисляются по формуле:
x0 = = = 3
y0 = y(x0) = 9 - 6*3 +5 = -4
Значит, координаты вершины : (3, -4)
c) Ось симметрии задается уравнением: x = 3
d) По теореме Виета:
Если x1, x2 - корни квадратного уравнения , ТО
Отсюда получаем корни x1 = 1; x2 = 5
Эти корни и есть нули функции
e) Дополнительные точки можно найти путем подстановки любых чисел: например, пусть x=0. тогда y = y(0) = 5
f) см прикрепленный рисунок
так как эти три числа образуют геометрическую прогрессию и их сумма равна 21,мы можем составить такое уравнение
далее, мы знаем, что для членов арифметической прогрессии верно утверждение
Запишем подряд члены получившеся арифметической прогрессии и применим для них это утверждение
тогда
получилась система из 2х уравнений с двумя неизвестными
решение очень громоздкое, но думаю, что с ним реально справиться.
Я выражал из первого b1 и подставлял во второе, в итоге получил 2 варианта
1 4 16 q=4
16 4 1 q=0,25
См объяснение
Объяснение:
а) так как перед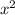 стоит положительный коэффициент (равный единице), следовательно ветви параболы направлены вверх
стоит положительный коэффициент (равный единице), следовательно ветви параболы направлены вверх
б) координаты вершины (x0, y0) вычисляются по формуле:
x0 =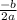 =
= 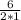 = 3
= 3
y0 = y(x0) = 9 - 6*3 +5 = -4
Значит, координаты вершины : (3, -4)
c) Ось симметрии задается уравнением: x = 3
d) По теореме Виета:
Если x1, x2 - корни квадратного уравнения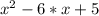 , ТО
, ТО
Отсюда получаем корни x1 = 1; x2 = 5
Эти корни и есть нули функции
e) Дополнительные точки можно найти путем подстановки любых чисел: например, пусть x=0. тогда y = y(0) = 5
f) см прикрепленный рисунок
так как эти три числа образуют геометрическую прогрессию и их сумма равна 21,мы можем составить такое уравнение
далее, мы знаем, что для членов арифметической прогрессии верно утверждение
Запишем подряд члены получившеся арифметической прогрессии и применим для них это утверждение
тогда
получилась система из 2х уравнений с двумя неизвестными
решение очень громоздкое, но думаю, что с ним реально справиться.
Я выражал из первого b1 и подставлял во второе, в итоге получил 2 варианта
1 4 16 q=4
16 4 1 q=0,25