1. Какие уравнения являются линейными: а) 2х-5у =7; б). 6х+4у = 0; в). х² - 3у = 8; г).ху + 4,5 х= -11?
2. Является ли решением уравнения х+ 3у=-7 пара чисел ( 2; -3), (-1; -2), ( 0;7/3), (-8,5;-0,5)?
3. Из уравнения -2х+5у=4 1). выразите: а) у через х; б). х через у. 2). Найдите два любых решения этого уравнения
ответ: 1-б. 2-а, 3-г, 4-, 5- , 6-в, 7-г
Объяснение:
1. Найдите значение алгебраической дроби 2х/х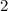
-1, при х= 1/3
• а) 0,75; б) -0,75 ; в) - ;г) -1,5
2. Найдите значение x, при котором дробь х+2/х-4 не имеет смысла
а)4 б)-2 в) -4 г) нет таких значений
3. Какое из предложенных выражений записано в виде алгебраической дроби?
а)2х/3+х ; б)2/х2+3х в)81х2/13-х ; г)2/3-х
4. Найдите значение выражения , при а= -0,7, в=0,3
а)2,5; б) -2,5; в) 1; г) другой ответ.
5.При каком значении а дробь не определена?
а) 0; б) - ; в) ; г)другой ответ.
6. Найди допустимые значения букв, входящих в дробь а/b
а) любые значения; б)5 возможных значений ; в) любые значения а и b, при b не равным 0 ; г) нет ответа
7.Выберите дробно- рациональные выражения 2х/3+4/7, 2-5х/7,3, 3/х-2
а) нет правильного ответа ; б) 2х/3+4/7 ; в)2-5х/7,3 ; г) 3/х-2
7 + 1 = 8 км/ч - скорость лодки по течению реки
7 - 1 = 6 км/ч - скорость лодки против течения реки
S = 20 км - расстояние по реке
t < 3 ч - время движения
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Пусть u км туристы плыли по течению, тогда (20 - u) км - против течения, затратив на весь путь меньше трёх часов. Составим неравенство по условию задачи:
u/8 + (20-u)/6 < 3
u · 6 + (20 - u) · 8 < 3 · 6 · 8
6u + 160 - 8u < 144
6u - 8u < 144 - 160
-2u < -16
-u < -8 ⇒ u > 8
20 - 8 = 12
ответ: 8 < u < 12.