Посмотрим промежутки возрастания-убывания функции, исследовав производную на знаки. Так как при разложении перед иксами коэффициенты равны 1 (4 можно отбросить, если мы поделим на неё, решая неравенство), то в крайнем правом промежутке "+", а дальше знаки будут чередоваться, но при переходе через x=0 чередования не будет, так как это нуль четной кратности (x²). Получим, что y'>0 при x>3/2, а y'<0 при x<3/2 (за исключением x=0). В x=0 и x=3/2 y'=0. Получается, что точка минимума в x=3/2.
Но мы рассматриваем отрезок [-2;1]. На нем функция только убывает.
Если я правильно понимаю, то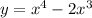
Посмотрим промежутки возрастания-убывания функции, исследовав производную на знаки. Так как при разложении перед иксами коэффициенты равны 1 (4 можно отбросить, если мы поделим на неё, решая неравенство), то в крайнем правом промежутке "+", а дальше знаки будут чередоваться, но при переходе через x=0 чередования не будет, так как это нуль четной кратности (x²). Получим, что y'>0 при x>3/2, а y'<0 при x<3/2 (за исключением x=0). В x=0 и x=3/2 y'=0. Получается, что точка минимума в x=3/2.
Но мы рассматриваем отрезок [-2;1]. На нем функция только убывает.
Значит, максимум в x=-2; минимум в x=1
2х+3 / х - 5х / х = 0
2х+3-5х / х = 0
3-3х / х = 0
ОДЗ: х≠0
3-3х=0
3х=3
х=1
2) х² / х-1 = 1 / х-1
х² / х-1 - 1 / х-1 = 0
х²-1 / х-1 = 0
(х-1)(х+1) / х-1 = 0
х+1 = 0
х = -1
3) 1 / х-1 - х / х+1 = х / х²-1
х+1 / (х-1)(х+1) - х(х-1) / (х+1)(х-1) - х / (х-1)(х+1) = 0
х+1-х²+х-х / (х-1)(х+1) = 0
х+1-х² / (х-1)(х+1) = 0
ОДЗ: (х-1)(х+1)≠0, х≠1, х≠ -1
х+1-х² = 0
х²-х-1=0
D=1+4=5
х₁ = 1-√5 / 2
х₂ = 1+√5 / 2
4) x^4-14x^2+13=0
x² = t
t²-14t+13=0
D = 196-52 = 144
t₁ = 14-12 / 2 = 1
t₂ = 14+12 / 2 = 13
х² = 1
х₁ = -1, х₂ = 1
х² = 13
х₃ = -√13, х₄ = √13