Поскольку кубик имеет 6 граней, при броске каждого кубика есть шесть возможных вариантов выпадения очков. если бросать два кубика одновременно, то количество разных вариантов выпадения очков на двух кубиках будет равно 6*6 = 36. теперь нам необходимо определить, какое количество вариантов соответствует случаю, когда сумма выпавших на двух кубиков очков будет равна 6. переберем все такие возможности: 1) 1 кубик - 1, 2 кубик - 5; 2) 1 кубик - 2, 2 кубик - 4; 3) 1 кубик - 3, 2 кубик - 3; 4) 1 кубик - 4, 2 кубик - 2; 5) 1 кубик - 5, 2 кубик - 1. всего таких вариантов 5, а общее число вариантов выпадения очков на двух кубиках равно 36, следовательно, вероятность того что при броске двух кубиков сумма выпавших очков будет равна 6 составит 5/36. ответ: искомая вероятность 5/36
-
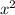+ 8х + 3х - 24 = -х (х - 3) + 8 (х - 3) = (х - 3) (8 - х)
-
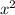- 11х + 2х + 22 = -х (х + 11) + 2 (х + 11) = (х + 11) (2 - х)
-
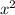- 17х + 3х + 51 = -х (х + 17) + 3 (х + 17) = (х + 17) (3 - х)
-2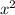
- 22х + 11х + 121 = -2х (х + 11) + 11 (х + 11) = (х + 11) (11 - 2х)
-4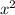
+ 10х - 12х +30 = -4х (х + 3) + 10 (х + 3) = (х + 3) (10 - 4х)
-5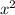
- 10х + 4х + 8 = -5х (х + 2) + 4 (х + 2) = (х + 2) (4 - 5х)
4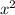
+ 16х - 5х - 20 = 4х (х + 4) - 5 (х + 4) = (х + 4) (4х - 5)
9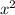
- 27х + 6х + 18 = 9х (х - 3) + 6 (х + 3)
В последнем, скорее всего, какая-то ошибка, потому что преобразовать его в произведение невозможно.