1. Найдите значение коэффициента к, если известно, что график функции у = x
через точку с координатами M(1; -5).
5).
A) 5 ; Б)1; B) -1; Г) - 5.
2.
2. Решите графическим методом систему уравнений
+ 0,5x=3,
2x - = 7;
3.
3. При каких значениях т точки ( - 5; m ) и В (m ; 16) лежат на графике
функции у =
4. Задайте формулой функцию, график которой проходит через точку (0; 5) и
параллелен графику функции у = -2х.
5. Выпишите из данных функций у= 5x+3 , = 4x +1, y = - x- 6 функцию ,
график которой
A) параллелен графику функции у = 4x - 2;
Б) пересекается с графиком функции у = 5x - 7;
B) перпендикулярен графику функции у= - 3x .
ответ обоснуйте .​

Объяснение:

7(5а + 8) - 11а= 35a+56 -11a= 24a +56

3(8а - 4) + 6а=24a - 12 +6a= 30a-12

9x + 3(15 - 8x)= 9x +45 - 24x = 45 -15x

11c + 5(8 - c)= 11c + 40 -5c =6c +40

13а - 8(7а - 1)= 13 a - 56a +8=8 -43a

7b - 2(3b - 1)= 7b - 6b +2 = b +2

8 – 6(2х-5) + (12х - 2)= 8- 12x +30 +12x -2=36

2(0,3b - 1) - (3b - 5)=0,6b - 2 - 3b +5= 3- 2,4b

3(0,9а - 1,5) - (За – 9)= 2,7 a -4,5- 3a+9 = 4,5 -0,3a

- (12y - 30у - 4)) +9y= -12y +30y +4 +9y=27y+4

-(4y - 9(2y - 1)) - 14y= -4y +18y -9 -14y = -9

a - (a - (2а - 4 ))= a - ( a -2a +4)= a-a+2a-4=2a -4

b - (b - (3b - 5))= b - (b-3b +5)= b - b +3b -5= 3b -5

7х-((у - x) +3y)= 7x - y +x +3y= 8x +2y

8а - (a - b) + b)= 8a -a +b +b= 7a+2b

2,8 5а -4(5 - а)= 2,85 a -20 +4a =6,85a -20

-3.5a -4 - 3(4 - а)= -3,5 a -4 -12 +3a=-0,5a- 16

-8a (-1,2- а) - (а - 2)= 9,6a +8a^2 -a+2= 8,6a +8a^2 +2

Объяснение:

Вынести общий множитель - значит у нескольких слагаемых , которые представляют из себя произведения (в твоём примере слагаемое  3ху - это произведение трёх множителей, один множитель = 3, второй = х, третий = у ;  а слагаемое 5у - произведение 5 и у ), найти общий (одинаковый) множитель и вынести его за скобку.

У слагаемых 3ху  и 5у  общим  множителем является "у". Его и надо вынести за скобку.

Что же останется в скобке ? Это легко узнать, разделив каждое слагаемое на вынесенный общий множитель.

Получим:    .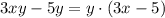

Проверить правильность действия легко, умножив множитель на полученную скобку.

Примеры.