1. Найдите значение коэффициента k, если известно, что график функции x
k
y
проходит
через точку с координатами А (4; 0). [1]
2. Найдите координаты точки пересечения функции y = −
1
2
x − 6 с осью абсцисс:
A) (
1
2
;0)
B) ( -
1
4
; 0)
C) (-3;0)
D) (-12;0)
[1]
3. Задайте формулой функцию, график которой проходит через точку (0; -1) и параллелен
графику функции y = 2x-3.
[3]
4. Социологи опросили 23 школьников, выясняя, сколько книг каждый из них прочел за
месяц. Были получены следующие данные:
3, 0, 1, 5, 1, 2, 3, 3, 1, 1, 3, 0, 3, 4, 2, 4, 5, 5, 6, 2,7,1,6.
a) Постройте таблицу абсолютных частот и таблицу относительных частот.
b) Укажите самое распространенное число прочитанных книг.
[4]
5. Решите графическим методом систему уравнений:
{
x − 2y = −1
2x + y = 3
примем всю работу за единицу
х-выполняет 1 бригада за 1 день
у-выполняет 2 бригада за 1 день
составим систему уравнений
12(х+у)=1 ⇒ 12х+12у=1 ⇒12х+12у=1 ⇒ вычитаем из первого второе
2х=3у 2х-3у=0 12х-18у=0
30у=1 у=1/30
значит вторая бригада за 1 день выполняет 1/30 всей работы.Значит ей нужно 30 дней,чтобы выполнить все работу
2х=3/30=1/10 х=1/20
значит первая бригада выполняет за 1 день 1/20 всей работы.Следовательно ей нужно 20 дней,чтобы выполнить всю работу
Пусть эти числа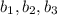 , тогда
, тогда
Сумма геометрической прогрессии из 3 членов равна:
или
Обозначим первое число арифметической прогрессии буквой а, тогда:
Сумма арифметической прогрессии 3 членов равна:
Сумма арифметической прогрессии равна будет сумме геометрической минус 48, раскроем:
Также сумма арифметической прогрессии равна простой сумме ее членов, т.е.:
Из последних двух уравнений найдем второй член прогрессии:
Нашли второй член прогрессии, он равен 15. Подставим в (1) уравнение, представив первый член через второй:
Получили два знаменателя геометрической прогрессии, через него выразим все числа через второй известный член прогрессии:
Получили возрастающую и убывающую прогрессии:
1) 3, 15, 75
2) 75, 15, 3
Это и будет ответом.
З.Ы. Можешь проверить на арифметической прогрессии (вычесть 48 из первого члена) и увидишь, что арифметические прогрессии тоже выполняются.