1.Найдите значение выражения: (2,6⋅0,3−2 4 :5 2 ) : (−1,9 )
15
3
2 Упростите выражение и найдите его значение:
0,7(2с – 9х) – 4(0,25с + х), если
с = 0,7 и х = –0,4
3.Решите уравнение:
0,2(7 – 2у) = 2,3 – 0,3(у – 6)
4 Постройте график функции у = 2х + 6
Пользуясь графиком функции найдите:
а) значение функции, если значение аргумента
равно 1,5;
б) значение аргумента, при котором значение
функции равно –2.
5.Представьте в виде степени выражение:
(
6
х3) ⋅х 4
2
)3
2
у ⋅у ⋅( у3⋅у )
18
; б)
х
6 Не выполняя построения, найдите координаты
точек, в которых график функции у = –0,45х + 9
пересекает каждую из координатных осей.
7 Постройте графики функций у = х + 4
и у = –3х в одной системе координат и укажите
координаты точки их пересечения.
И. Сикорский создал первые отечественные самолеты и вертолет. Для доставки людей и грузов, особенно в труднодоступные районы или в случаях это весьма значимо!
З. Ермольева получила отечественный пенициллин и стрептомицин - первые антибиотики жизнь людей, особенно в условиях войны!
С. Лебедев создал электронную вычислительную машину - облегчит труд ученых при создании сложных систем (ракет)
Н.Никитин построил Останкинскую телебашню, которая служит уже 50 лет для телевещания России.
+ открытия И. Павлова, Н.Вавилова
Благодаря С. Королеву русские первыми побывали в космосе и сейчас летают.
4 км/ч
Объяснение:
Строим таблицу скорость, время, расстояние.
Т.к. нам необходимо найти изначально запланированную скорость, то
обозначим её за x:
v t S
1) нач. x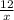 12
12
2) с зад. x+2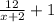 12
12
Расстояние 12км.
Т.к. v*t=S, то t=S/v t1=12/x
Во втором случае время на 1 час больше.
Приравниваем t1 и t2+1:
По пропорции, учитывая, что x≠0 и x≠-2:
12(x+2)=x(14+x)
12x+24=14x+x²
x²+2x-24=0
D=4+96=100
Т.к. время не может быть отрицательным, то подходит x=4 км/ч .