1. Назовите верное высказывание *
1) Если a>b, то b 2) Если a>0, то a/3 > a/2
3) Если b 4) Если -×>1, то ×>-1
2. Даны два неравенства а) (×-3)(×+1)>(×-1)^2 б) x^2+2×+1×≥4× Назовите неравенства, верные при любых значениях x. *
1) а, б
2) а
3) б
4) нет верного ответа
3. Известно,что 4 ≤ a ≤ 5, 2 ≤ b ≤ 3. Оцените границы выражения 2a-b. В ответе укажите сумму целых значений выражения 2a-b, принадлежащим границам этого выражения. *
1) 13
2) 26
3) 20
4) 21
4. Округлите число до единиц и найдите относительную погрешность округления 8,536 *
1) 8%
2) 6,7%
3) 10%
5. Приближенное значение числа x равно a. Найдите абсолютную погрешность приближения, если x=2.76 a=2.8 *
1) 0,4
2) 0,04
3) 2
Сделаем вид, что оба корня существуют, возведем обе части в квадрат, найдем корни, а потом проверим их прямой подстановкой.
Возводим в квадрат:
Отсюда получаем три корня: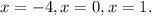
Подставим их в исходное уравнение (разделенное на 5 для удобства):
Да, под корнем одинаковые числа. Однако, так как корень из отрицательного числа не определен на множестве действительных чисел, х = -4 не является корнем уравнения.
Аналогичная ситуация. х = 0 не является корнем уравнения.
ОТВЕТ: {1}.
√(6x - 2y - 7) = (3x - y)/4 + 1
3x - y = t
√(2t - 7) = t/4 + 1
одз 2t - 7 ≥ 0 t ≥ 3.5
t/4 + 1 ≥ 0 t ≥ - 4
t ≥ 3.5
возводим в квадрат
2t - 7 = t²/16 + t/2 + 1
32t - 112 = t² + 8t + 16
t² - 24y + 128 = 0
D = 24² - 4*128 = 576 - 512 = 64
t12 = (24 +- 8)/2 = 16 8 оба корня проходят
подставляем во 2 уравнение
(x - 11y - 8)/(3x - y - 16) = x - y
1. t = 3x - y = 16
знаменатель получается 0
нет решений
2. t = 3x - y = 8
y = 3x - 8
( x - 33x + 88 - 8)/(3x - 3x + 8 - 16) = x - 3x + 8
-32x + 80 = 16x - 64
48x = 144
x = 3
y = 9 - 8 = 1
ответ (3, 1)