Докажем сначала, что если x и y - натуральные числа и удовлетворяют этому уравнению (кстати, это частный случай диофантова уравнения, которое называют уравнением Ферма или уравнением Пелля), то либо x либо y делятся на 3 (точнее, ровно одно из них делится на 3, но для нашего решения это не важно). В самом деле, если x и y не делятся на 3, то
то есть не может равняться 1. (число A получилось после вынесения общего множителя 3).
Итак, x или y делится на 3. Но по условию x и y - простые, поэтому x или y
равен 3.
1-й случай.
Поскольку 2 - простое число, получили решение (3;2).
(3;2)
Объяснение:
Докажем сначала, что если x и y - натуральные числа и удовлетворяют этому уравнению (кстати, это частный случай диофантова уравнения, которое называют уравнением Ферма или уравнением Пелля), то либо x либо y делятся на 3 (точнее, ровно одно из них делится на 3, но для нашего решения это не важно). В самом деле, если x и y не делятся на 3, то
Итак, x или y делится на 3. Но по условию x и y - простые, поэтому x или y
равен 3.
1-й случай.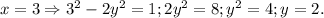
Поскольку 2 - простое число, получили решение (3;2).
2-й случай.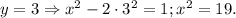
Такое уравнение не имеет решений в целых числах.
Объяснение:
Пусть y = 2 , тогда x² = 9 и x = 3 , если x = 2 , то 2y² = 3 , а
полученное уравнение решений в натуральных числах не
имеет , пусть x ≠ 2 и y ≠2 , тогда x и y - нечетные числа :
x = 2k + 1 и y = 2m + 1 , подставим эти выражения в исходное
уравнение : 4k² +4k +1 - 2( 4m² + 4m + 1) = 1
или : 4k²+ 4k -8m²-8m = 2 ⇒ 2( k²+k - 2m² -2m ) = 1 , но
полученное уравнение не имеет решений в натуральных
числах , так как левая часть кратна 2 , а правая нет ⇒ ( 3 ; 2 )
- единственная пара простых чисел , удовлетворяющая
исходному уравнению