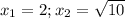1.Порівняйте a і b, якщо
1). а – b = 5; 2). a – b = -4.1
2. Дано f(x) = +−. Знайдіть: 1) f(0); 2) f(3).
3. Розв'яжіть нерівність:
1). -3х<12; 2). 4х – х2 ≥ 0.
4. Знайдіть дев'ятий член та суму перших десяти членів врифметичної прогресії
(аn), якщо а1=9, d=-2
5. Розв'яжіть систему рівнянь: {х−у=, {х−ху−у
6. Побудуйте графік функції у = х2+ 4х – 5. За графіком знайдіть:
1) область значень функції;
2) проміжок зростання функції.
7. Доведіть, що х2+ у2 - 2(2х – у) + 5≥0 для будь - яких значень х і у.
Чтобы прибавить, или отнять дроби с разными знаменателями, мы приводим к наименьшему общему знаменателю, и прибавляем(или отнимаем)
Если числитель и знаменатель дроби умножить или разделить на одно и тоже натуральное число, то получится равная ей дробь.
Это значит разделить и числитель и знаменатель на одно и то же число, не равное нулю. Например дробь 2/4 сокращаем на два:1/2.5/10 сокращаем на 5=1/2
незнаю, наверное до бесконечности
Дробь называют несократимой тогда, когда сократить эту дробь невозможно...
Сори, времени сейчас нет, дальше не могу решать..
Пусть большее простое число из T(x) равно n.Сравним числа:n^2 и 2T(x),то есть квадрат наибольшего простого числа и удвоенную сумму простых чисел до n:
Очевидно,что все простые числа,кроме 2 нечетные,а значит T(x) меньше суммы двойки и натуральных нечетных чисел от 1 до n(так как не все нечетные числа являются простыми).
Рассмотрим данную сумму,члены которой,кроме двойки образуют арифметическую прогрессию.
Сравним 2S и n^2
Правая часть больше левой(нуля) при:
А так как S>T(X) и n^2>2S,то n^2>2T(x)
Значит и x^2>2T(x) при n,указанном выше.
Рассмотрим оставшиеся 2 варианта:
n=2 n=3
ответ: