1. Постройте график линейной функции: у=-2х+1 с графика найдите: а) наименьшее и наибольшее значение функции на отрезке [-1; 3,5 ] б) значение переменной Х, при которых У=0 и У>0. 2. Найдите координаты точки пересечения прямых у=-х и у=х-2.

3. а) найдите координаты точки пересечения графика линейного уравнения 2х-5у-10=0 с осями координат б)определите, принадлежит ли графику данного уравнения точка М(- 1,5; -2,6)

4. а) задайте линейную функцию у=kх формулой, если известно, что ее график параллелен прямой 4х+у+7=0 б)определите возрастает или убывает заданная функция. ответ объясните.

5. При каком значении p решение уравнения -pх+2у+p=0 является пара чисел (-1; 2) ?
ДА ЖЕ УЖЕ!

Первообразная (F(x)) - это функция (а не точка), которая ищется интегрированием другой функции (f(x))

Объяснение:

Находим интеграл от (3x-2)^8, для этого преобразовываем дифференциал (dx). добавляем 1/3 * 3 и тройку заносим под знак дифференциала: d(3x), 1/3 остаётся за интегралом. Константу можно добавить "просто так", ведь производная простого числа - 0, и получаем d(3x-2). Далее интегрируем это выражение как одну переменную: интеграл от а равен а^2/2. здесь интеграл от а^8 = а^9/9. Получаем ответ, не забываем С

Примем за 1 - объем цистерны

Пусть t цис./ч - производительность "медленного" насоса.

Тогда 3t цис./ч - производительность "быстрого" насоса.

(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.

(t+3t)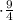 - объем работы системы из двух насосов за 2ч 15мин.

Получим уравнение: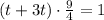

9t = 1

Значит,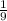 - цис./ч - производительность "медленного" насоса.

Тогда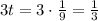 - цис./ч - производительность "быстрого" насоса.

Следовательно,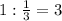 ч - потребуется "быстрому" насосу на заполнение цистерны.

ответ: 3 ч.