1. Предположив, что центры сторон треугольника находятся в точках (5: 2), (2, -3), (2; 1), найдите эти вершины. A) A (1: 2) B (7: 6) C (5: 6) B) A (5: -2) B (5: 6) (-1; -4) C) A (3; 2) B (6; 5) C (-3; 4) D) A (0; 2) B (65) C (5; 6) E) A (4,5) B (3,4) (-6; 7) 2. Решить неравенство: 4x2x2 5 20. . А) (1; 6). В) (6; 4). В) Нет ответа. Г) (3; 5). E) (1; 8). > 0. x + 5 3. Найдите правильное решение неравенства: A) 5: +00) B) 6-00: -5) c) (-0,5) D) (-00; 5] E) (-53 + 00 ) 4. Решите неравенство: (x + 13) (x - 7)? (x - 15-0 A) (-00; -13) B) (- 60; -13) (15; +0) C) (-13; 7) (15; to) D) (15; +0 ) E) (-13: 15) 5. y- 1 = 5 - x? Найдите радиус круга. А) 1 Б) + -6 В ​

Пусть вкладчик положил рублей в банк. Через год вкладчик получит 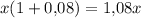рублей. После того, как снял деньги, у него остается 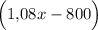рублей. Известно, что на счёте осталась сумма, равная половине первоначального вклада. Составим уравнение

В конце второго года хранения вкладчик получит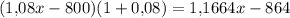 рублей. Подставив значение х, получим 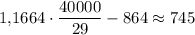рублей.

ответ: на счету у вкладчика в конце второго года хранения будет 745 рублей.

1. q = -2.

2. 1;1/2;1/4 q = 1/2

1;3;9q = 3

2/3;1/2;3/8q = 3/4

√2; 1;√2/2q = 1/√2

3.  заданная формула возможно неточно переписана или последовательность не геометрическая.

3*2n - 3 умножить на 2n или 3 возвести в степень 2n

4. q  = 0,5

5.  S = -0.25

6. b6 = 243.

7. 3-n,3-2n,3-3n,3-4n, 3n,3n+1,3n+2,3n+3 - єти последовательности не являются геометрическими прогрессиями

Объяснение:

1. Последовательность геометрическая т.к. а2 = а1 * q,  а3 = а2 * q, где

q - одно и тоже число (знаменатель данной геометрической прогрессии)

q = а2 / а1 = -6 / 3 = -2.

4. Из формулы нахождения n-го члена геометрической прогрессии

q = а2 / а1 = 10/20 = 0,5.

5. q = а2 / а1 = -2/4 = -0,5

а5 = 4 * (-0,5)^4 = 0.25

a4 = 4 * (-0.5) ^3 = -0.5

6. b6 = b1 * q^5 = 243.