1.Преобразовать в многочлен: а) (с – 7)2; в) (6x – 5)(6x + 5);
б) (2m + n)2; г) (3d + 2y)(3d – 2y).
2. Разложить на множители:
а) c2 – 25; в) 64c2d4 – 4n6;
б) m2 + 8a + 16; г) (x + 2)2 + (x – 2)2.
3. Упростить выражение:
(x – 5)2 – 4x(x + 3).
4. Решите уравнение:
а) (x – 2)(x + 2) – x(x + 5) = – 8;
б) 25y2 – 16 = 0.
5. Выполнить действия:
а) (4y2 + 9)(2y – 3)(2y + 3);
б) (7m2 – 3n3)(7m2 + 3n3).

Решение
1)  2sin x-1=0
sinx = 1/2
x = (-1)^n arcsin(1/2) + πk, k∈Z
x = (-1)^n (π/6) + πk, k∈Z
2)  cos(2x+П/6)+1=0
cos(2x+П/6) = - 1
2x+П/6 = π + 2πn, n∈Z
2x = π - π/6 + 2πn, n∈Z
2x = 5π/6 + 2πn, n∈Z
x = 5π/12 + πn, n∈Z
3)  6sin²x - 5cosx + 5 = 0
6(1 - cos²x) - 5cosx + 5 = 0
6 - 6cos²x - 5cosx + 5 = 0
6cos²x + 5cosx - 11 = 0
cosx = t, ItI ≤ 1
6t² + 5t - 11 = 0
D = 25 + 4*6*11 = 289
t₁ = (- 5 - 17)/12
t₁ = - 22/12
t₁ = -11/6
t₁ = - 1 (5/6) не удовлетворяет условию ItI ≤ 1
t₂ = (- 5 + 11)/12
t₂ = 1/2
cosx = 1/2
x = (+ -)arccos(1/2) + 2πm, m∈Z
 x = (+ -) *(π/3) + 2πm, m∈Z

Примем за 1 - объем цистерны

Пусть t цис./ч - производительность "медленного" насоса.

Тогда 3t цис./ч - производительность "быстрого" насоса.

(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.

(t+3t)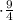 - объем работы системы из двух насосов за 2ч 15мин.

Получим уравнение: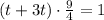

9t = 1

Значит,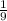 - цис./ч - производительность "медленного" насоса.

Тогда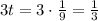 - цис./ч - производительность "быстрого" насоса.

Следовательно,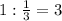 ч - потребуется "быстрому" насосу на заполнение цистерны.

ответ: 3 ч.