1. Приведите примеры множеств. 2. Как обозначают множество и его элементы? 3. Как обозначают множества натуральных, целых и рациональных чисел? 4. Как записать, что элемент a принадлежит множеству A? Не принадлежит множеству А? 5. Какие существуют задания множеств? 6. Какое множество называют подмножеством данного множества? 7. Как наглядно иллюстрируют соотношение между множествами? 8. Какое множество является подмножеством любого множества? 9. Какое множество называют собственным подмножеством данного множества?
Как решаются такие уравнения.
Правило звучит таким образом.
В первую очередь нужно перенести в одну сторону от знака равенства все слагаемые, содержащие переменную, а все числовые слагаемые перенести в другую сторону от знака равенства.
Например, во втором 2) примере:
переносим 2х влево, а 4 вправо. При переносе через знак равно меняется знак слагаемого на противоположный.
То есть получаем:
9х + 2х = 48 - 4.
Вычисляем правую и левую части:
11х=44.
После этого находим х, делим правую и левую части уравнения на множитель при х, то есть на 11.
11х / 11 = 44 / 11
х = 4. Это ответ.
в 5) делаем аналогично:
переносим слагаемые с х в одну сторону, числа в другую:
в данном случае перенесем 1.3х вправо, чтобы знак у слагаемого с х был плюс:
6.8 + 2.7 = 0.6х + 1.3х
9.5 = 1.9х
Чтобы дальше решалось проще, умножим правую и левую части на 10 (удобно так избавляться от дробей)
9.5*10=1.9х*10
95 = 19х
Теперь делим правую и левую части на 19:
95/ 19 = 19х / 9
5 = х
х = 5
Развернуть уравнение можно в любой момент в процессе решения.
ответ: х = 5.
6) решается аналогично:
переносим слагаемые с переменным влево, числовые слагаемые вправо:
4/9 * х - 1/6 * х = 9 - 14 = -5, сразу вычисляем правую часть
Для упрощения вычисления умножим правую и левую часть уравнения на 18 - наименьшее число такое, умножение на которое позволит избавиться от дробей в левой части:
4/9 * х * 18 - 1/6 * х * 18 = -5 * 18
4*18/9 * х - 1*18/6 * х = -80
18 делим на 9, получаем 2; 18 делим на 6, получаем 3.
4*2*х - 1*3*х = -80
8х - 3х = -80
5х = -80
Делим правую и левую части на 5:
5х/5 = -80/5
х = -18
ответ: х = -18
Дана функция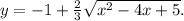
Начнём с выражения под корнем.
Минимум по производной равен: 2х - 4 = 0, х = 2.
Под корнем 4 - 4*2 + 5 = 1.
Минимум всей функции равен -1 +(2/3)*1 = -1/3.
Перенесём -1 влево и возведём обе части уравнения в квадрат.
(у + 1)² = (4/9)(x² - 4x + 5).
В правой части выделим полный квадрат.
x² - 4x + 5 = (x² - 4x + 4) - 4 + 5 = (x - 2)² + 1.
Правая часть примет вид (4/9)((x - 2)² + 1) = (4/9)(x - 2)² + (4/9).
Перенесём квадрат с х влево:
(у + 1)² - (4/9)(x - 2)² = 4/9.
Разделим обе части на 4/9.
((у + 1)²)/(4/9) - ((x - 2)²/1) = 1.
Получили уравнение гиперболы, повёрнутой на 90 градусов.
Но в соответствии с заданием, только верхняя часть этой гиперболы удовлетворяет заданному уравнению.