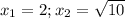1. Продовжити речення. Центр кола, описаного навколо будь-якого трикутника, лежить у точці перетину……. . Побудувати це коло і трикутник.
2. Навколо трикутника АВС з кутами <А=300 і <С=900 описане коло. Знайдіть його радіус, якщо СВ = 12см.
3. Два кола мають зовнішній дотик, а відстань між їх центрами дорівнює 15см. Знайдіть радіуси цих кіл, якщо вони відносяться, як 2:3.
4. В трикутник вписане коло, X, Y, Z – точки дотику кола відповідно сторін АВ, ВС, АС. Знайти довжину відрізка CY, якщо BY=5см, AX=7см, а периметр ∆АВС дорівнює 32см.
(x - 2)(x ^ 2 + |x - 1|) - x ^ 2 + 2x = 0 x ^ 3 + x|x - 1|- 2x ^ 2 - 2x| * x - 1| - x ^ 2 + 2x = 0 x ^ 3 + x
x|x - 1|- 3x ^ 2 - 2x| * x - 1| + 2x = 0 x ^ 3 + x
x * (x - 1) - 3x ^ 2 - 2(x - 1) + 2x = 0,
x - 1 >= 0 x ^ 3 + x(- (x - 1)) - 3x ^ 2 - 2x * (- (x - 1)) + 2x = 0
x - 1 < 0 x = 2 x = - 1,
x >= 1 x = 1 х = 1 х = 2 ,
X <1 x = 1 x = 2 x
x = 1 x = 2 Рішення x 1 =1,x 2 =2
x/(x + 5) - (1x + 51)/(5 - x) = 50/(x ^ 2 - 25) x/(x + 5) - (1x + 51)/(5 - x) = 50/(x ^ 2 - 25), x = - 5, x = 5 x/(x + 5) - (x + 51)/(5 - x) = 50/(x ^ 2 - 25) x/(x + 5) - (x + 51)/(5 - x) * 50/(x ^ 2 - 25) = 0 x/(x + 5) * (x + 51)/(- (x - 5)) * 50/((x - 5)(x + 5)) - 0 x/(x + 5) + (x + 51)/(x - 5) - 50/((x - 5)(x + 5)) = 0 (x(x - 5) + (x + 5)(x + 51) - 50)/((x - 5)(x + 5)) = 0 (x ^ 2 - 5x + x ^ 2 + 51x + 5x + 255 - 50)/((x - 5)(x + 5)) = 0 (2x ^ 2 + 41x + 10x + 205)/((x - 5)(x + 5)) = 0 (x(2x + 47) + 5(2x + 47))/((x - 5)(x + 5)) = 0 ((2x + 41)(x + 5))/((x - 5)(x + 5)) = 0 (2x + 41)/(x - 5) = 0 2x + 41 = 0 2x = - 41 x=- 41 2 ,x=-5.x=5 Рішення x = - 41/2 Альтернативна форма 1 1 x = - 20 - x=-20 5
Пусть большее простое число из T(x) равно n.Сравним числа:n^2 и 2T(x),то есть квадрат наибольшего простого числа и удвоенную сумму простых чисел до n:
Очевидно,что все простые числа,кроме 2 нечетные,а значит T(x) меньше суммы двойки и натуральных нечетных чисел от 1 до n(так как не все нечетные числа являются простыми).
Рассмотрим данную сумму,члены которой,кроме двойки образуют арифметическую прогрессию.
Сравним 2S и n^2
Правая часть больше левой(нуля) при:
А так как S>T(X) и n^2>2S,то n^2>2T(x)
Значит и x^2>2T(x) при n,указанном выше.
Рассмотрим оставшиеся 2 варианта:
n=2 n=3
ответ: