1.разложи на множители tz4−tm−uz4+dm+um−dz4 2.вычисли: - вопрос №144421294831833146129839946911 от Alisa66611 16.10.2021 09:24

Question

Алгебра: 1.разложи на множители tz4−tm−uz4+dm+um−dz4 2.вычисли: 129⋅48−31⋅83−31⋅46+129⋅83

Alisa66611 · Answer

Нам потребуется следующая

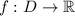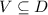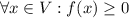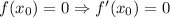Л е м м а: пусть функция $f: D\to \mathbb{R}$ дифференцируема на некотором открытом множестве $V\subseteq D$ , причем $\forall x\in V:f(x)\geq 0$ . Тогда $f(x_{0}) = 0 \Rightarrow f'(x_{0}) = 0$ .

Д о к а з а т е л ь с т в о: в общем-то следует из необходимого условия локального экстремума: легко видеть, что точка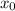 $x_{0}$ является локальным минимумом.

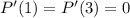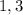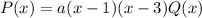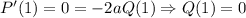Любой многочлен, конечно, является дифференцируемой функцией. Потому P'(1) = P'(3) = 0 . Более того, поскольку 1,3 -- корни многочлена, то P(x) = a(x-1)(x-3)Q(x) . Продифференцируем: $P'(x) = a\left[(x-3)Q(x)+(x-1)Q(x)+(x-3)(x-1)Q'(x)\right]$ . В точке производная равна $P'(1) = 0 = -2aQ(1)\Rightarrow Q(1) = 0$ , аналогично в точке 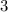: 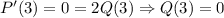$P'(3) = 0 = 2Q(3) \Rightarrow Q(3) = 0$ . С другой стороны, 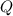-- многочлен второй степени, а потому 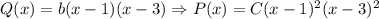$Q(x) = b(x-1)(x-3) \Rightarrow P(x) = C(x-1)^2(x-3)^2$ . 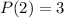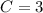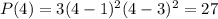Поскольку P(2) =3 , то C = 3 , следовательно, P(4) = 3(4-1)^2(4-3)^2 = 27 .