Площадь - это число, показывающие сколько места занимает фигура. Площадь вычисляется с произведения. Для того, чтобы найти площадь, нужно ширину умножить на длину. У квадрата все стороны равны, а значит ширина равна длине. Имея эти данные, мы можем вычислить его стороны. В условии сказано, что одна из сторон равна 4 м., а стало быть и остальные равны 4 м. Теперь мы можем вычислить площадь квадрата(учитывая то, что ширина равна длине). Обозначается площадь латинской буквой S:
Но это ещё не всё. Площадь измеряется в квадратах. К примеру: см², мм², м², и т.д.
Так как в условии даны м., значит и площадь будет м².
Площадь - это число, показывающие сколько места занимает фигура. Площадь вычисляется с произведения. Для того, чтобы найти площадь, нужно ширину умножить на длину. У квадрата все стороны равны, а значит ширина равна длине. Имея эти данные, мы можем вычислить его стороны. В условии сказано, что одна из сторон равна 4 м., а стало быть и остальные равны 4 м. Теперь мы можем вычислить площадь квадрата(учитывая то, что ширина равна длине). Обозначается площадь латинской буквой S:
Но это ещё не всё. Площадь измеряется в квадратах. К примеру: см², мм², м², и т.д.
Так как в условии даны м., значит и площадь будет м².
ответ: 16 м²
Вертикальные асимптоты: x = 2
Горизонтальные асимптоты: y = 3
Нет наклонных асимптот
Объяснение:
Выясним, при каких значениях переменной функция 3 x + 1 x − 2 не определена. x = 2
Рассмотрим рациональную функцию
1. Если n < m , то ось x, y = 0 , является горизонтальной асимптотой.
2. Если n = m , то горизонтальной асимптотой является прямая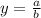
Если n > m , то не существует горизонтальной асимптоты (только наклонная асимптота).
Найдем n и m
n = 1 ; m = 1
Поскольку n = m , горизонтальная асимптота является прямой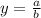
, где a = 3 и b = 1
y = 3
Наклонных асимптот нет, поскольку степень числителя меньше либо равна степени знаменателя.
Это множество всех асимптот.
Вертикальные асимптоты: x = 2
Горизонтальные асимптоты: y = 3
Нет наклонных асимптот