1. Разложите на множители:
1) a3 + 64b3;
2) a* - 16;
3) х2у-81y2;
4) 5m2 - 10mn +5n2;
5) 4ab - 28b + 8a - 56.
2. Упростите выражение (3а + 1)(9a2 -3а + 1) и найдите значение при а =2/3.
3. Разложите на множители:
1) x3 - 8x2 + 16x;
2) n + 5+ n2 - 25;
3) ab5 - b5-ab3 + b3.
4. Решите уравнение:
1) 6x3 - 24x = 0;
2) 49x3 + 14x2 + x = 0;
3) x3 - 5x2 - x + 5 = 0.
5. Вычислите, используя формулы сокращенного умножения: 173 2 - 2 • 173 • 73 + 73 2
6. Известно, что а - b = 6, ab = 5. Найдите значение выражения (a + b)2.
ответ:решение ниже
Объяснение:
пусть меньшая сторона площадки a= x, тогда бОльшая сторона равна b=(x+2)
площадь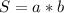
=x*(x+2)=120 м.кв
откроем скобки и решим квадратное уравнение
корень равный -12 не подходит поскольку размер не может быть отрицательным значением.
Получаем что:
сторона площадки а = 10 м - меньшая
сторона площадки b=10+2=12 м - бОльшая
сумма длин всех сторон площадки даст ответ на вопрос сколько необходимо бордюра, сумма длин всех сторон есть периметр
P=a+b+a+b=10+12+10+12=44 м
Если в одной упаковке 8 метров материала, то чтобы посчитать количество упаковок, необходимо требуемую длину разделить на объем упаковки:
44/8=5, 5 упаковок.
т.е. для построения бордюра потребуетсz 6 упаковок
ответ:решение ниже
Объяснение:
пусть меньшая сторона площадки a= x, тогда бОльшая сторона равна b=(x+2)
площадь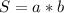
=x*(x+2)=120 м.кв
откроем скобки и решим квадратное уравнение
корень равный -12 не подходит поскольку размер не может быть отрицательным значением.
Получаем что:
сторона площадки а = 10 м - меньшая
сторона площадки b=10+2=12 м - бОльшая
сумма длин всех сторон площадки даст ответ на вопрос сколько необходимо бордюра, сумма длин всех сторон есть периметр
P=a+b+a+b=10+12+10+12=44 м
Если в одной упаковке 8 метров материала, то чтобы посчитать количество упаковок, необходимо требуемую длину разделить на объем упаковки:
44/8=5, 5 упаковок.
т.е. для построения бордюра потребуетсz 6 упаковок