1. Решить систему уравнений методами: обратной матрицы, Крамера, Гаусса 4. Вычислить пределы: 5.Найти производные: 6.Провести полное исследование функции y = f(x) и построить ее график.
Покажем на рисунке необходимые величины. Ось X направим по направлению движения. Так как скорость спринтера растёт, то ускорение направлено также по движению (по скорости). Это можно понять, если проанализировать формулу (6) – вектор v будет увеличиваться, если он направлен по вектору a ! Впрочем, если ты не знаешь, куда направить ускорение – ничего страшного – направляй куда-нибудь (в этой задаче, естественно, либо по движению, либо против). Знак ответа даст тебе правильное направление: если получится (+), то ускорение было направлено правильно, ну а если (–), то в другую сторону.
Запишем формулы (6) и (7) в проекции на ось X для данной задачи:
v A=at ; S= at 2
По условию начальная скорость v0=0 , а так как все вектора 2 направлены по оси X, то везде знаки (+). Из первой формулы можно найти ускорение a=vtA =5 м/с2 , подставляя которое во вторую формулу получим перемещение (и путь, так как движение происходит вдоль прямой в одну сторону): S=10м .
Сравним значения функций в данных точках. Для этого достаточно посмотреть на знак их разности : если он положительный, то ; если равен нулю, то значения равны; иначе .
По предположению, , поэтому вторая скобка отрицательна.
Если , то сумма меньше -16, тогда первая скобка тоже отрицательна, а всё произведение положительно и Получили, что большему значению аргумента соответствует большее значение функции, тогда на отрезке функция возрастает.Аналогично, для произведение отрицательно. Здесь большему значению аргумента соответствует меньшее значение значение функции, по определению это значит, что функция убывает.
Путь (S) = 10 м
Ускорение (а) = 5м/с2
Объяснение:
Покажем на рисунке необходимые величины. Ось X направим по направлению движения. Так как скорость спринтера растёт, то ускорение направлено также по движению (по скорости). Это можно понять, если проанализировать формулу (6) – вектор v будет увеличиваться, если он направлен по вектору a ! Впрочем, если ты не знаешь, куда направить ускорение – ничего страшного – направляй куда-нибудь (в этой задаче, естественно, либо по движению, либо против). Знак ответа даст тебе правильное направление: если получится (+), то ускорение было направлено правильно, ну а если (–), то в другую сторону.
Запишем формулы (6) и (7) в проекции на ось X для данной задачи:
v A=at ; S= at 2
По условию начальная скорость v0=0 , а так как все вектора 2 направлены по оси X, то везде знаки (+). Из первой формулы можно найти ускорение a=vtA =5 м/с2 , подставляя которое во вторую формулу получим перемещение (и путь, так как движение происходит вдоль прямой в одну сторону): S=10м .
Возьмем две точки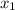 ,
, 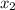 , причем
, причем 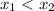 .
.
Им соответствуют значения функции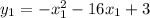 и
и 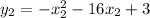 .
.
Сравним значения функций в данных точках. Для этого достаточно посмотреть на знак их разности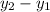 : если он положительный, то
: если он положительный, то 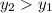 ; если равен нулю, то значения равны; иначе
; если равен нулю, то значения равны; иначе 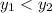 .
.
По предположению,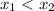 , поэтому вторая скобка отрицательна.
, поэтому вторая скобка отрицательна.
Если