1. Самостоятельная работа
Задание 1. Выполнить умножение
а) (х – 3)(х + 3) б) (5 – у)(5 + у) в) (х + 2у)(2у – х) г) (- а + 2)(а + 2)
д) (8а + 9с)(9с – 8а)
Задание 2. Разложить на множители
а) 64 – х² б) – 9у²+ х² в) 1,21 – х² г) 36 – у² д) -25х²+ у²
е) а²– 0,04
Объяснение:
в 3 раза больше значит, чем w - значит 3*w
в первом w роз + 19 роз (добавили), во втором 3w + 17
если их стало поровну, то значит они равны
и получилось уравнение:
w+19=3w+7
-2w= -26
w= 13 роз в первом букете
3*13=39 роз во втором букете
ответ: 13 и 39
неизвестно, сколько деталей производит ученик, но мастер производит в 4 раза больше
неизвестное обозначаем как x
следовательно, ученик - x деталей, мастер 4х деталей
а вместе изготовили они 300 деталей
x+4x=300
5x=300
x=60 деталей изготовил ученик
4x=4*60=240 деталей изготовил мастер
ответ: 60 и 240
#1. Функция задана формулой
1.1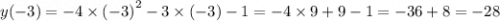
1.2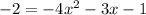
1.3 x = - 1, y = - 2, подставляем значения в функцию, если равенство будет верным, то значит точка А(-1; - 2) принадлежит графику функции. (в 1.2 мы нашли корни уравнения, при y=-2, x=-1, значит точка принадлежит графику функции, но, всё же, распишу так: )
равенство верное, точка принадлежит графику функции.
#2. Используя график функции укажите:
2.1 Область определения функции: [-4.5; 5]
2.2 Область значения функции: [-2.5; 4.5]
2.3 Промежутки возрастания функции: [-4.5; 1], промежутки убывания функции: [1; 5]
#3.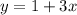 .
.
Это линейная функция, формула которой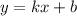 , где
, где
если k > 0, то функция возрастающая, если k < 0, то функция убывающая.
У нас k = 3, 3 > 0 => функция возрастающая.
#4. Найти область определения функции:
4.1
Область определения:
4.2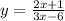
знаменатель не должен быть равным нулю: ,
, 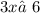 ,
, 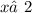
Область определения: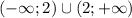
4.3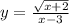
в числителе корень, число под корнем не должно быть отрицательным: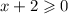 ,
, 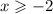
знаменатель не должен быть равным нулю: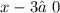 ,
, 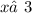
Область определения: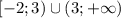
4.4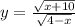
в числителе корень, число под корнем не должно быть отрицательным: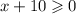 ,
, 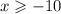
в знаменателе корень, число под корнем не должно быть отрицательным; знаменатель не должен быть равным нулю: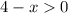 ,
, 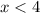
Область определения: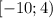
#5. Разложить на множители квадратный трёхчлен. Можно это сделать по формуле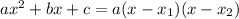 , где
, где 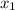 и
и 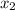 — корни уравнения
— корни уравнения 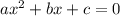 .
.
5.1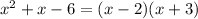
5.2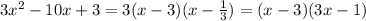
#6. Найти значение дроби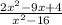 при
при  .
.
Для начала нужно упростить дробь.
Разложим квадратный трёхчлен из числителя на множители, по формуле из задания 5.
В знаменателе разность квадратов, используем формулу сокращенного умножения.
В итоге,
#7. а)