1. схематически построй какую-нибудь функцию, нули которой равны -1 и 6.

2. начерти какой-нибудь график, у которого:
а. область определения – [-2; 5];
б. область значений – [-1; 7];
в. нули функции – 1 и 3.

3. начерти какой-нибудь график, у которого: а. область определения – [-4; 1]; б. область значений – [-5; 0]; в. промежуток возрастания – [-2; 1]

4. найдите область определения функции: y= 4−√9−3x/(x+1)(1−2x)

5. при каких значениях a функция y=−(3−2a)x+4:
а. возрастает;
б. убывает.

a) cos(a-b) - cos(a+b) = cos(a)*cos(b) + sin(a)*sin(b) - (cos(a)*cos(b) - sin(a)*sin(b)) = cos(a)*cos(b) + sin(a)*sin(b) - cos(a)*cos(b) + sin(a)*sin(b) = 2sin(a)*sin(b)

b) sin(2a) + cos(2a) + 1 = 2*sin(a)*cos(a) + cos²(a) - sin²(a) + cos²(a) + sin²(a) = 2*sin(a)*cos(a) + 2*cos²(a) = 2*cos(a)*(sin(a) + cos(a))

sin() = -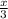

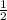
= arcsin(-) + 2πκ, κ∈Ζ

или

= π - arcsin(-) + 2πn, n∈Ζ

= - + 2πκ, κ∈Ζ

= π + + 2πn, n∈Ζ

= + 2πn, n∈Ζ

x₁ = -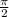 + 6πκ, κ∈Ζ

x₂ =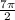 + 6πn, n∈Ζ

Отбор корней произведем с неравенств.

x₁: 0 ≤ 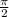 - + 6πκ ≤ 3π

≤ 6πκ ≤ 3π +

≤ 6πκ ≤

≤ 6κ ≤

≤ κ ≤

Так как κ∈Ζ, то  κ∈∅

x₂: 0 ≤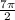   + 6πn ≤ 3π

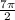- ≤  6πn ≤ 3π -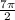

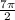- ≤  6πn ≤ -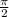

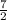- ≤  6n ≤ -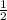

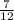- ≤  n ≤ -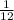

Так как n∈Ζ, то  n∈∅ ⇒ нет корней на данном промежутке

Хорошо, давайте решим задачу.

Мы должны изобразить множество решений неравенства (х+1)² + (у-2)² ≤ 4 на координатной плоскости. Для этого следуйте этим шагам:

Шаг 1: Рассмотрим неравенство в его исходной форме:
(х+1)² + (у-2)² ≤ 4

Шаг 2: Заметим, что неравенство представляет уравнение окружности с центром (-1, 2) и радиусом 2. Это связано с тем, что в левой части неравенства мы имеем квадрат расстояния от точки (х, у) до центра окружности.

Шаг 3: Теперь нарисуем координатную плоскость и отметим центр окружности (-1, 2).

Шаг 4: Далее, проведем окружность с центром (-1, 2) и радиусом 2. Для этого нам нужно отметить точки окружности, которые находятся на расстоянии 2 от центра.

Шаг 5: Чтобы найти эти точки, мы можем использовать уравнение окружности в общем виде: (x-a)² + (y-b)² = r², где (a, b) - координаты центра окружности, а r - радиус окружности.

В нашем случае, уравнение окружности будет иметь вид: (x+1)² + (y-2)² = 2²

Шаг 6: Подставим x = -1 и y = 2 в уравнение окружности и найдем r²: (-1+1)² + (2-2)² = 0 + 0 = 0. Значит, r² = 4.

Шаг 7: Теперь, используя радиус окружности и ее центр, проведем окружность на координатной плоскости.

Шаг 8: Наконец, чтобы найти множество решений неравенства, нужно ограничить площадь внутри окружности, так как мы имеем неравенство с знаком "меньше или равно". Это означает, что все точки, находящиеся внутри окружности или на ней, удовлетворяют неравенству.

Итак, мы изобразили множество решений неравенства (х+1)² + (у-2)² ≤ 4 на координатной плоскости в виде окружности с центром (-1, 2) и радиусом 2.