Рассмотрим сразу числитель: sin 10 cos 55 + sin 280 sin 55 = sin 10 cos 55 + sin (270 + 10) sin 55 = [формулы приведения] = sin 10 cos 55 + (-cos 10) sin 55 = [sin (a-b) = sin a cos b - sin b cos a] = sin (10 - 55) = sin (-45) = - sin 45 = -√2/2 Знаменатель: sin 10 cos 110 + sin 260 cos 200 = sin 10 cos (90 + 20) + sin (270 - 10) cos (180 +20) = sin 10 (-sin 20) + (-cos 10) (-cos 20) = cos 10 cos 20 - sin 20 sin 10 = [cos(a+b) = cos a cos b - sin a sin b] = cos (10+20) = cos 30 = √3/2 Все выражение: √6 * (-√2/2) / (√3/2) = -√6*√2*2 / (2√3) = -√2 * √2 = -2
Примем за 1 - объем цистерны
Пусть t цис./ч - производительность "медленного" насоса.
Тогда 3t цис./ч - производительность "быстрого" насоса.
(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.
(t+3t)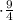
- объем работы системы из двух насосов за 2ч 15мин.
Получим уравнение: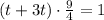
9t = 1
Значит,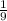
- цис./ч - производительность "медленного" насоса.
Тогда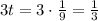
- цис./ч - производительность "быстрого" насоса.
Следовательно,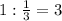
ч - потребуется "быстрому" насосу на заполнение цистерны.
ответ: 3 ч.
sin 10 cos 55 + sin 280 sin 55 = sin 10 cos 55 + sin (270 + 10) sin 55 = [формулы приведения] = sin 10 cos 55 + (-cos 10) sin 55 = [sin (a-b) = sin a cos b - sin b cos a] = sin (10 - 55) = sin (-45) = - sin 45 = -√2/2
Знаменатель:
sin 10 cos 110 + sin 260 cos 200 = sin 10 cos (90 + 20) + sin (270 - 10) cos (180 +20) = sin 10 (-sin 20) + (-cos 10) (-cos 20) = cos 10 cos 20 - sin 20 sin 10 = [cos(a+b) = cos a cos b - sin a sin b] = cos (10+20) = cos 30 = √3/2
Все выражение:
√6 * (-√2/2) / (√3/2) = -√6*√2*2 / (2√3) = -√2 * √2 = -2