1.Сколько положительных членов имеет арифметическая прогрессия: 8,5; 8; 7,5 ...?
2.В геометрической прогрессии (bn) установите соответствие:
1) b4 = 10, b5 = 30, q -?
2) b1 = 2, q = 3, b5 -?
3) b6 = 486, q = 3, b1 -?
4) b1 = 2, b4 = -54, q -?
А) -3;
Б) 2
В) 3;
Г) 63;
Д) 162;
3.Вычислить сумму 0,1 +0,01+ 0,001+ 0,0001+...
1. 1) положителен
2. 3) невозможно определить знак.
Объяснение:
приведенное квадратное уравнение имеет вид
коэфициент при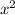
: a=1;
по теореме Виета :
свободный член
второй коэфициент
поэтому в случае 1 ответ 1) положителен, так как произведение двух чисел одинакового знака дает положительное число (плюс на плюс дает плюс и минус на минус дает плюс)
в случае 2 ответ 3) неозможно определить знак, так как к примеру при корнях -5 и 7 получим что второй коэффициент равен -2, а при корнях -7 и 5 получим что второй коэффициент равен 2
2. Степенью многочлена называют наибольшую из степеней входящих в него одночленов.
4. Слагаемые, имеющие одинаковую буквенную часть, называют подобными слагаемыми.
5. Многочлен стандартного вида - многочлен, все одночлены которого приведены к стандартному виду.
6. Сумма многочленов равна многочлену, членами которого являются все члены данных многочленов.
7. Разность многочленов есть многочлен, членами которого являются все члены уменьшаемого и взятые с противоположными знаками все члены вычитаемого.
8. Если перед скобками стоит знак " + " , то можно опустить скобки и этот знак " + " , сохранив знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках записано без знака, то его надо записать со знаком " + " .
Чтобы раскрыть скобки, перед которыми стоит знак " – " , надо заменить этот знак на " + " , поменяв знаки всех слагаемых в скобках на противоположные, а потом раскрыть скобки.
Чтобы записать сумму, противоположную сумме нескольких слагаемых, надо изменить знаки данных слагаемых.
9. Чтобы найти произведение многочлена на одночлен надо каждый член многочлена умножить на этот одночлен.
11. Вынесение общего множителя за скобки.
12.Чтобы найти произведение многочленов, надо каждое слагаемое одного многочлена умножить на каждое слагаемое другого многочлена
13. Разложить многочлен на множители – это значит преобразовать его в произведение двух или более многочленов
14. Целое выражение – это математическое выражение, составленное из чисел и буквенных переменных с действий сложения, вычитания и умножения.