1.Уравнение 18x2 +5x−7=0 является неприведённым приведённым
2.Найди корни неполного квадратного уравнения
(Сначала вводи больший корень.)
X= ;X=
3.Реши неполное квадратное уравнение 4 x 2 +8x=0
(первым вводи больший корень).
X= ; X=
4.Найди корни неполного квадратного уравнения 4 x 2 −36x=0
(первым вводи меньший корень).
x=
x=
5.Реши уравнение (x−2)(x+10)=0 (Ввод начни с наибольшего корня уравнения).
ответ: x 1 = x 2 =
6.Найди дискриминант квадратного уравнения 7 x 2 +14x+5=0
ответ: D=
7.Определи число корней квадратного уравнения 21 x 2 +4x+7=0 .
Нет корней Нет верного ответа Два корня Три корня
8.Найди корни квадратного уравнения x 2 +7x+12=0 (первым вводи больший корень; если корни одинаковые, впиши ответ в оба окошка). x 1 = ; x 2 = .
9.Реши квадратное уравнение 5 x 2 −8x+3=0 . Корни: x 1 = ; x 2 = (первым вводи больший корень).
10.Найди дискриминант квадратного уравнения 3 x 2 +14x+15=0 . ответ: D= .
11.Определи число корней квадратного уравнения 21 x 2 +5x+3=0 . Два корня Нет корней Нет верного ответа Три корня
12.Найди корни квадратного уравнения x 2 +8x+15=0 (первым вводи больший корень; если корни одинаковые, впиши ответ в оба окошка). x 1 = ; x 2 = .
13.Реши квадратное уравнение 5 x 2 −23x+12=0 . Корни: x 1 = ; x 2 = (первым вводи больший корень).
14.Реши квадратное уравнение 4 x 2 −11x+6=0 . Корни: x 1 = ; x 2 = (первым вводи больший корень).
15.Реши квадратное уравнение 2 (10x−9) 2 −5(10x−9)+2=0 (первым вводи больший корень): x 1 = ; x 2 = . Дополнительный во какой метод рациональнее использовать? Разложение на множители Метод введения новой переменной Раскрытие скобок Вынесение за скобку
16.Найди корни уравнения 7,3(x−9)(x+2,4)=0 . (Первым пиши меньший корень.) x= ; x= .
17.Реши квадратное уравнение x 2 −4x+3=0 (первым вводи больший корень). x 1 = ; x 2 = .
2sinxcosx-√3cosx=0
cosx(2sinx-√3)=0
cosx=0⇒x=π/2+πn,n∈Z
sinx=√3/2⇒x=(-1)^n*π/3+πk,k∈Z
б)sin 2x=√2 cos x
2sinxcosx-√2cosx=0
cosx(2sinx-√2)=0
cosx=0⇒x=π/2+πn,n∈Z
sinx=√2/2⇒x=(-1)^n*π/4+πk,k∈Z в)sin(0,5п+x)+ sin 2x=0
г)cos(0,5п+x)+ sin 2x=0
-sinx+2sinxcosx=0
-sinx(1-2cosx)=0
sinx=0⇒x=πn,n∈Z
cosx=1/2⇒x=+-π/3+2πk,k∈Z
д)sin 4x+√3 sin 3x+sin 2x=0
2sin3xcosx+√3sin3x=0
sin3x(2cosx+√3)=0
sin3x=0⇒3x=πn,n∈Z⇒x=πn/3,n∈Z
cosx=-√3/2⇒x=+-5π/6+2πk,k∈Z
е)cos 3x+sin 5x=sin x
cos3x+sin5x-sinx=0
cos3x+2sin2xcos3x=0
cos3x(1+2sin2x)=0
cos3x=0⇒3x=π/2+πn,n∈Z⇒x=π/6+πn/3,n∈Z
sin2x=-1/2⇒2x=(-1)^(k+1)*π/6+πk,k∈Z⇒x=(-1)^(n+1)*π/12+πk/2,k∈Z
№1) 1)0.25x>1 2)1-6x>=0 3)5y-7-6< 4y-1.5
x>1/0.25 6x=<1 y<11.5
x>4 x<=1/6
№2)
m+1<3m-18
-2m< -19
m> 9.5
№3
А)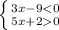 Б)
Б) 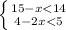
ответ: x принадлежит {-0.4 ; 3} ответ: X больше 1
№4
Б)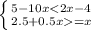
1; 2; 3; 4; 5
ОДЗ