Відповідь:
Пояснення:
1. f(x)=4+x^5
f'(x)=x^4>=0 для всех х → во всей области определения f(x) возрастает, так как производная на всей области больше 0, не отрицательная
2. f(x)= -6/x+9 области определения f(x) : xєR & x≠0
f'(x)=6/x^2 >0
Так как производная на всей области определения >0, то функция возрастающая
1). f(x)=4-x^3 области определения f(x) : xєR
f'(x)=-3х^2<0
Так как производная на всей области определения <0, то функция убивающая
2) f(x)=5/x-11 области определения f(x) : xєR & x≠0
f'(x)= -5/x^2 <0
1)(x-1)(2x-3)<0
(x-1)(2x-3)=0
Рисунки увидишь на фото ниже
ответ:x∈(1;1.5)
2)(x+3)(x-1)≥0
(x+3)(x-1)=0
ответ:x∈(-∞;-3] v [1;+∞)
3) 5(x- )(x+4)>0
5(x- )(x+4)=0 ⇒x=;x=-4
ответ:x∈(-∞;-4)v(;+∞)
(Бро,прости 4 могу не правильно решить)
5)(3x + 1)(x + 3) < 0
3x+1=0
x=
и
x+3=0
x=-3
ответ:x∈(-3;)
6)(5x - 3)(2x + 7) ≥ 0
ответ:x∈(-∞;-3,5]v[0,6;+∞)
Объяснение:
Відповідь:
Пояснення:
1. f(x)=4+x^5
f'(x)=x^4>=0 для всех х → во всей области определения f(x) возрастает, так как производная на всей области больше 0, не отрицательная
2. f(x)= -6/x+9 области определения f(x) : xєR & x≠0
f'(x)=6/x^2 >0
Так как производная на всей области определения >0, то функция возрастающая
1). f(x)=4-x^3 области определения f(x) : xєR
f'(x)=-3х^2<0
Так как производная на всей области определения <0, то функция убивающая
2) f(x)=5/x-11 области определения f(x) : xєR & x≠0
f'(x)= -5/x^2 <0
Так как производная на всей области определения <0, то функция убивающая
1)(x-1)(2x-3)<0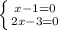
(x-1)(2x-3)=0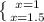
Рисунки увидишь на фото ниже
ответ:x∈(1;1.5)
2)(x+3)(x-1)≥0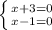
(x+3)(x-1)=0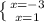
Рисунки увидишь на фото ниже
ответ:x∈(-∞;-3] v [1;+∞)
3) 5(x-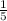
)(x+4)>0
5(x-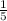
)(x+4)=0 ⇒x=
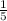;x=-4
Рисунки увидишь на фото ниже
ответ:x∈(-∞;-4)v(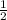
;+∞)
(Бро,прости 4 могу не правильно решить)
5)(3x + 1)(x + 3) < 0
3x+1=0
x=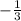
и
x+3=0
x=-3
ответ:x∈(-3;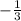
)
Рисунки увидишь на фото ниже
6)(5x - 3)(2x + 7) ≥ 0
ответ:x∈(-∞;-3,5]v[0,6;+∞)
Объяснение: