1) в прямоугольном параллелепипеде боковое ребро 5см,площадь диагонального сечения равна 205 см кв. ,а площадь основания 360 см кв. найти стороны основания. 2) основанием пирамиды служит параллелограмм со сторонами 3 и
7 см и одной из диагоналей 6 см. высота пирамиды 4 см и проецируется в точку пересечения диагоналей основания. найти боковые рёбра пирамиды. 3) в конусе, у которого высота и радиус основания равны 23 см, проведена через
вершину плоскость, отсекающая от окружности основания дугу в 90 градусов. найти площадь полученного сечения. 4) сторона основания правильной четырёхугольной пирамиды и её высота равны 4 дм. найти радиус описанного
около неё шара. 5) найти площадь боковой поверхности правильной шестиугольной призмы, наибольшая диагональ которой равна 13 дм, а боковое ребро 5 дм. 6) найти площадь полной поверхности правильной четырёхугольной
пирамиды, если её высота равна 20 см, а сторона основания 42см. 7) найти площадь полной поверхности равностороннего цилиндра, если площадь его боковой поверхности равна q см кв. 8) высота усечённого конуса равна 6 см,
радиусы оснований 10 и 2 см. найти площади его боковой и полной поверхности. 9) диаметр шара равен 20 см, высота его сегмента 6 см. найти площадь сферической поверхности сегмента и его объём.

Показать ответ

Ответ:

priss666

24.05.2020 14:25

2. по теореме пифагора находим одно из ребер 9+16=25

по формуле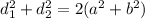 d_1^2 + d_2^2=2(a^2+b^2) (если что там между d1 и d2 знак + и между а и b знак +) 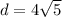$d=4\sqrt{5}$ дальше так же по теореме пифагора считаем оставшееся ребро пирамиды и оно будет равно 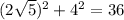$(2\sqrt{5})^2+4^2=36$ (эта штука опять зажевала +) а это значит что само ребро равно 6