1. В треугольнике ABC BC>AC. Какие углы треугольника можно сравнить по этим данным?
1) A и B.
2) A и C.
3) B и C.
4) Нельзя сравнить.
2. В треугольнике DEF DF 1) D 2) F 3) E>D.
4) F>E.
3. В треугольнике KLM KM>LM>KL. Какое неравенство при этом выполняется?
1) M 2) L 3) L>K>M.
4) K>M>L.
4. Сравните стороны треугольника MON, если O 1) OM=ON 2) MN>MO>NO.
3) MO=MN 4) MN 5. В треугольнике XYZ сторона XY наибольшая. Каким может быть угол X?
1) Тупым, или прямым, или острым.
2) Тупым или прямым.
3) Острым.
4) Прямым или острым.
6. Какая сторона треугольника лежит против тупого угла?
1) Наибольшая.
2) Наименьшая.
3) Средняя по величине.
4) Нельзя определить.
7. Какая сторона треугольника лежит против острого угла?
1) Наибольшая.
2) Наименьшая.
3) Средняя по величине.
4) Нельзя определить.
8. В равнобедренном треугольнике две стороны равны 7 см и 14 см. Найдите его периметр
1) 21 см.
2) 28 см.
3) 35 см.
4) 42 см.
9. Периметр равнобедренного треугольника равен 63 см. Одна его сторона в три раза больше другой. Найдите боковую сторону треугольника.
1) 9 см.
2) 18 см.
3) 27 см.
4) 54 см.
10. Определите вид треугольника, если известно, что у него один внешний угол прямой.
1) Прямоугольный.
2) Тупоугольный.
3) Остроугольный.
4) Нельзя определить.
11. Определите вид треугольника, если известно, что у него один внешний угол острый.
1) Прямоугольный.
2) Тупоугольный.
3) Остроугольный.
4) Нельзя определить.
12. Определите вид треугольника, если один из его внутренних углов больше суммы двух других углов.
1) Прямоугольный.
2) Тупоугольный.
3) Остроугольный.
4) Нельзя определить.
13. Определите вид треугольника, если один из его внешних углов равен внутреннему углу.
1) Прямоугольный.
2) Тупоугольный.
3) Остроугольный.
4) Нельзя определить.
14. В прямоугольном треугольнике две стороны равны 20 см и 13 см. Какая из них является гипотенузой?
1) 13 см.
2) 20 см.
3) Нельзя определить.
15. Сколько наклонных можно провести из данной точки к данной прямой?
1) 1.
2) 2.
3) 4.
4) Бесконечно много.
16. Сколько наклонных заданной длины можно провести из данной точки к данной прямой?
1) 1.
2) 2.
3) 4.
4) Бесконечно много.
17. Из точки E к прямой a проведены перпендикуляр EH и наклонные EA, EB, EC. Причем известно, что AH=HB и точка C лежит между точками H и B. Сравните длины наклонных.
1) EA 2) EA 3) EA=EB 4) EC 18. Из точки F проведены к прямой b перпендикуляр FO, две равные наклонные FM, FN и наклонная FL, причем луч FM является внутренним лучом угла OFL. Сравните проекции данных наклонных.
1) LM>MO=NO.
2) LM 3) OL>OM=ON.
4) ON=OL 19. Сравните медиану треугольника с его периметром.
1) Меньше полупериметра.
2) Меньше периметра.
3) Больше полупериметра.
4) Нельзя определить.
20. Укажите точку, сумма расстояний от которой до вершин выпуклого четырехугольника будет наименьшей.
1) Разность арифметической прогрессии: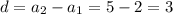 . Тогда по формуле n-го члена арифметической прогрессии, найдем четырнадцатый член:
. Тогда по формуле n-го члена арифметической прогрессии, найдем четырнадцатый член:
2) Пятый член: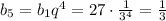
Сумма четырех первых членов геометрической прогрессии:
3) Знаменатель прогрессии:
Сумма бесконечно убывающей геометрической прогрессии:
4) Здесь в условии опечатка, скорее всего d=-0.5, а если так как есть то задача решения не имеет.
ответ: 7
5)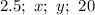 - геометрическая прогрессии
- геометрическая прогрессии
6) 6; 12; .... ; 96; 102; 108; .... ;198 - последовательность чисел, кратных 6.
Посчитаем сколько таких чисел:
Сумма первых 33 членов а.п.: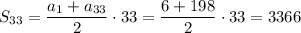
Нам нужно найти сумму всех натуральных чисел превышающих 100 и меньших 200 , которые кратны 6
, значит найдем сумму не превышающих 100 и отнимем от суммы не превышающих 200
Искомая сумма: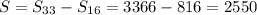
Находим производную: 4x^3 - 12x^2 +12x - 4
Приравниваем к нулю: 4x^3 - 12x^2 +12x - 4 = 0
Затем,чтобы получить красивую группировку,заменяем некоторые члены как сумму:
4x^3 - 8x^2 - 4x^2 + 8x + 4x - 4=0
(4x^3 - 4x^2) +(- 8x^2 + 8x) +( 4x - 4)=0
4x^2 (x-1) -8x (x-1) + 4 (x-1)= 0
(x-1)(4x^2-8x+4)=0
Поработаем отдельно со 2 множителем, разделим на 4
и получим X^2 - 2x +4=0
(x-1)^2=0
Теперь,получаем произведение равно нулю,либо первый множитель равен нулю,либо второй,
получаем корни
x=1 и x=-1(не входт в указанный промежуток)
Теперь считаем заначения,подставляя их в функцию
f(0)= -9
f(1) = -10 (наим)
f(4) = 71 (наиб)