1) В уравнении 3x²-6x=11 найдите сумму его коэффициентов

а) 8 в) -14

б) 14 г) 20

2) Какое из уравнений не имеет корней:

1) x²-6x=0;
2) x²-7=0;
3) 3x2²+4=2x²-7;

4) 6x²-11=-8.

а) 1; 2 в) 3

б) 2; 3 г) 4

3) Решите уравнение: 2/7 x²-5x=0.

а) 2/35 в) 17,5

б) 0; 2/35 г) 0; 17.5

4) Решите квадратное уравнение: (5-4x)²=121

а) -1,5 ; -4 в) 1,5 ; 4

б) -3/2 ; 4 г) 1,5 ; -4

5) Уравнение 2x²-4x-m=0 имеет только один корень. Чему равно значение m?

а) m=2 в) m=4

б) m= -2 г) m= -4

6) Уравнение x²+bx-c=0 Имеет 2 корня: 2 и 3.

Чему равны коэффициенты b и c?

а) b= -5, c= -6 в) b= -5, c=6

б) b=5, c= -6 г) b=5, c=6

7) Составьте квадратное уравнение с корнями -√18 и √2

а) x²-2√2 x+6=0
в) x²-2√2 x-6=0

б) x²+2√2 x-6=0
г) x²+√20 x-6=0

8) Дано уравнение x²-9x+6=0. Чему равна сумма квадратов корней уравнения.

а) 69 в) 96

б) 45 г) 54

9) При каких значениях m и n корнями уравнения mx²+nx+3=0

являются числа 1 и -3?

а) m=1, n=2 в) m= -1, n=2

б) m= -1, n= -2 г) m=1, n= -2

10) При каких значениях m уравнение x²+x-m+1=0 не имеет корней

а) m>0.75
в) m-любое число

б) m<0.75
г) уравнение всегда имеет корни

Показать ответ

Ответ:

ВРотКомпот

17.03.2020 02:37

Рассмотрим множество A, заданное в условии:

$A=\{\frac{1}{3k} :k \in \mathbb {N}\}$

и множество натуральных чисел ℕ. Замечу, что при любом k дробь вида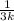 $\frac{1}{3k}$ является несократимой, то есть если выписывать такие дроби, начиная с k = 1 и увеличивая каждый раз переменную k на 1, ни одна из них не повторится (так как знаменатель постоянно увеличивается).

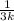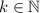Покажем, что между этими двумя множествами можно установить взаимно однозначное соответствие. Для этого всем дробям вида $\frac{1}{3k}$ , где $k \in \mathbb {N}$ , поставим в соответствие число 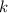. С одной стороны, согласно построению каждой такой дроби будет соответствовать натуральное 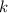, притом единственное. С другой стороны, для каждого натурального 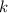можно указать единственную (смотри замечание в предыдущем абзаце) дробь вида 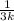$\frac{1}{3k}$ , и все они будут принадлежать множеству A, поскольку 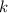пробегает все натуральные значения. Итак, построенное соответствие действительно взаимно однозначное. А раз множество ℕ счетное, то и множество A также счетное.