1 вариант №1. Постройте график линейной функции
y=-2х + 1. С графика найдите:
а) значение у, если х = 3;
б) значение хесли у = -1;
№2. Найдите координаты точки пересечения
прямых у = 3-хиу = 2х.
3. Функция задана формулой у= 6х + 19.
Определите, проходит ли график функции через
точку А(-2; 7).
№4. Известно, что график функции y=kx+
проходит через точку С(2;5). Найдите значение k.
№5. Постройте график функции
-2x +1 если х -2
у = kx +1 если – 2 9 – х если х> 1

Показать ответ

Ответ:

kkatya3082

02.01.2021 23:00

Множество M={ 1 ,2 ,3 ,4 ,5 }

Всех двухэлементных подмножеств пятиэлементного множества М будет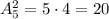 $A_{5}^2=5\cdot 4=20$ штук, если учитывать порядок следования элементов . Это такие элементы: 12, 13, 14, 15, 21 , 23, 24, 25, 31, 32, 34, 35, 41, 42, 43, 45, 51, 52, 53, 54 . Здесь элементы 12 и 21 , 34 и 43 и т.д. считаются разными ( как числа) .

Всех двухэлементных подмножеств пятиэлементного множества М будет $C_{5}^2=\dfrac{5\cdot 4}{2!}=10$ штук, если не учитывать порядок следования элементов . Это такие элементы: 12, 13, 14, 15,23, 24, 25, 34, 35, 45 . Здесь элементы 12 и 21 , 34 и 43 и т.д. считаются одинаковыми, то есть учитывается только то, что, например, первый элемент множества содержит 1 и 2 , восьмой элемент множества содержит 3 и 4 , в любом порядке, поэтому записываем либо пару цифр (1,2) , либо пару (2,1) .

0,0(0 оценок)

Ответ:

xotmirov1

13.04.2021 09:02

Чтобы упростить заданные выражения, сначала необходимо раскрыть скобки, для этого умножим значение перед скобками на каждое значение в скобках, а потом приведем подобные слагаемые:

1) 3 * (2х + 1) + 5 * (1 + 3х) = 3 * 2x + 3 * 1 + 5 * 1 + 5 * 3x = 6х + 3 + 5 + 15х = 21х + 8;

2) 4 * (2 + х) - 3 * (1 + х) = 4 * 2 + 4 * x - 3 * 1 - 3 * x = 8 + 4х - 3 - 3х = х + 5;

3) 10 * (n + m) - 4 * (2m + 7n) = 10 * n + 10 * m - 4 * 2m - 4 * 7n = 10n + 10m - 8m - 14n = 2m - 4n;

4) 11 * (5c + d) + 3 * (d + c) = 55c + 11d + 3d + 3c = 58c + 14d.

0,0(0 оценок)

Популярные вопросы: Алгебра