Смотри, cos120 нету (в таблице), а найти его значение нужно, то мы используем круг и его четверти. Смотреть картинки. Весь круг это 360 градусов, тоесть если нам нужно найти sin390 мы это расписываем sin390=sin(360+30)=sin30 360 градусов это круг, мы возвращаемся к исходу: 0 градусов. Значит тот остаток в виде 30 градусов мы и считаем его.
Также от этого зависимы и значение + и - (Смотреть картинки). Мы ищем sin120, во второй чверти его значение + , значит sin того градуса который мы получили будет иметь знак +
Чверти считают от начала отсчета (от 0 градусов)
В правой части равенства ставят этот знак имеющий левая часть выражения при условии, что альфа острый угол.
Если в левой части выражения \ формулы аргумент выглядит ± α ; ± α , то функция sin меняется на cos; ctg на tg; и наоборот; а если аргмент выглядит π ± α; 2π ± α функция не меняется.
Объяснение:
Собственная скорость Vc= х км/ч.
Против течения :
t₁ = S/(Vc- Vт) = 18 / (x-3) (ч.)
По течению:
t₂= S/ (Vc+Vт) = 48/ (x+3) (ч.)
Всего:
t₁+t₂=3 (ч.)
18/(х-3) + 48/(х+3) = 3 |× (x-3)(x+3)
18(x+3) + 48(x-3) = 3(x-3)(x+3)
18x+54 + 48x - 144= 3(x²-9)
66x -90 = 3x² - 27 |÷3
22x - 30 = x²-9
x²-9 -22x+30=0
x²-22x+21=0
D= (-22)² -4*1*21 = 484-84=400 ; √D= 20
x₁= (22 -20) /2 =2/2=1 - не удовл. условию, т.к. скорость лодки не может быть меньше течения реки
x₂= (22+20)/2= 42/2=21 (км/ч) Vc
ответ: Vc= 21 км/ч.
Смотри, cos120 нету (в таблице), а найти его значение нужно, то мы используем круг и его четверти. Смотреть картинки. Весь круг это 360 градусов, тоесть если нам нужно найти sin390 мы это расписываем sin390=sin(360+30)=sin30 360 градусов это круг, мы возвращаемся к исходу: 0 градусов. Значит тот остаток в виде 30 градусов мы и считаем его.
Также от этого зависимы и значение + и - (Смотреть картинки). Мы ищем sin120, во второй чверти его значение + , значит sin того градуса который мы получили будет иметь знак +
Чверти считают от начала отсчета (от 0 градусов)
В правой части равенства ставят этот знак имеющий левая часть выражения при условии, что альфа острый угол.
Если в левой части выражения \ формулы аргумент выглядит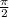
± α ;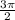 
± α , то функция sin меняется на cos; ctg на tg; и наоборот; а если аргмент выглядит π ± α; 2π ± α функция не меняется.