1) Выразить переменную у через переменную х
А) - 2х + у =15; б) 2у – 4х = 6; в) 11х – у = -7
2) Построить график уравнения 2х +у -3 = 0
(подсказка: выразить у через х, составить таблицу из 2 точек и по этим точкам на
координатной плоскости провести прямую)

Объяснение:

Когда основания одинаковые, то вот что с умножением и делением:

а² * а³ =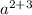 (например)

а³ : а² =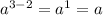 (например)

Когда показатели одинаковые, то вот:

а² + б² = (а + б)²

а² - б² = (а - б)²

а² : б² = (а : б)²

а² * б² = (а * б)²

Когда минус:

-а² = -(а * а)

(-а)² = (-а * -а)² (если показатель чётный, то на выходе будет положительное число, если не четный, то отрицательное)

Несколько степеней:

(а²)³ =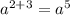

1. а)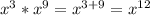

б)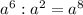

в)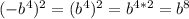

2.

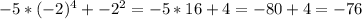
3. а)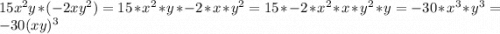

б)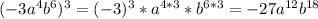

4.

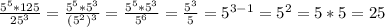
Извини, остальные не успеваю, надеюсь я понятно объяснил и ты сможешь их сам решить(

Даны координаты вершины треугольника ABC :А(1;0) ,В(13;-19),С(17;13) найти уравнение стороны АВ и АС и их угловые коэффициенты.

Находим векторы.

АВ = В(13;-19) - А(1;0) = (12; -19). По координатам вектора сразу определяется угловой коэффициент прямой АВ.

к(АВ) = Δу/Δх = -19/12.

Уравнение АВ: (x- 1)/12 = y/(-19) каноническое, или

                          19x + 12y - 19 = 0 общего вида, или

                           у = (-19/12)х + (19/12)   с угловым коэффициентом.

АС = С(17;13) - А(1;0) = (16; 13). По координатам вектора сразу определяется угловой коэффициент прямой АС.

к(АС) = Δу/Δх = 13/16.

Уравнение АС: (x- 1)/16 = y/13) каноническое, или

                          13x - 16y - 13 = 0 общего вида, или

                           у = (13/16)х - (13/16)   с угловым коэффициентом.