Решение ищем в виде произведение двух ненулевых функций:
Подставляем в уравнение:
Предположим, что сумма первого и третьего слагаемого в левой части равна 0:
Тогда, второе слагаемое в левой части равно правой части:
Общее решение:
Частное решение. Пусть :
Решение ищем в виде произведение двух ненулевых функций:
Подставляем в уравнение:
Предположим, что сумма первого и третьего слагаемого в левой части равна 0:
Тогда, второе слагаемое в левой части равно правой части:
Общее решение:
Частное решение. Пусть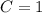 :
: