Пусть скорость автобуса равна х км/ч, а скорость легковой машины - у км/ч. По условию, y - x = 12. Тогда время затраченное автобусом равно , а легковым автомобилем - на весь путь время затрачено часов. Зная, что легковая машина пришла в город В на 5 мин раньше, чем автобус, составим систему уравнений
Умножив левую и правую части уравнения на 3x(x+12) ≠ 0.
1 час 45 минут = 105 мин
1 час 15 минут = 75 мин
2 час 55 минут = 175 мин
Пусть 1 - объем всего бассейна;
x - производительность первой трубы;
y - производительность второй трубы;
z - производительность третьей трубы;
t - производительность четвертой трубы
1) По условию первая, вторая и третья трубы наполняют бассейн за 105минут, значит, их совместная производительность равна:
2) Аналогично находим совместную производительность первой, второй и четвёртой труб:
3) Находим совместную производительность третьей и четвёртой труб:
Сложим полученные уравнения:
И, наконец, получим время, за которое заполнится бассейн, если открыть все 4 трубы:
ответ: 70 мин= 1 ч 10 мин
Пусть скорость автобуса равна х км/ч, а скорость легковой машины - у км/ч. По условию, y - x = 12. Тогда время затраченное автобусом равно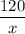 , а легковым автомобилем -
, а легковым автомобилем - 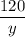 на весь путь время затрачено
на весь путь время затрачено 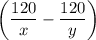 часов. Зная, что легковая машина пришла в город В на 5 мин раньше, чем автобус, составим систему уравнений
часов. Зная, что легковая машина пришла в город В на 5 мин раньше, чем автобус, составим систему уравнений
Умножив левую и правую части уравнения на 3x(x+12) ≠ 0.
По теореме Виета
Скорость легкового автомобиля: 60 + 12 = 72 км/ч.
ответ: 60 км/ч и 72 км/ч.