1. Является ли равенство (k+v)^2=(v+k)^2 тождеством? Докажи.
После тождественных преобразований
в левой части получишь выражение: k_ _ _k _ + _ ^2.
В правой части получится выражение: v_ _ _vk+ _ ^2.
Вывод: равенство является/не является тождеством.

2. Является ли равенство (5+x)(8+x)=x^2+13x+40 тождеством? Докажи.
После тождественных преобразований в левой части получится выражение:
• x^2−13x+40
• 40+5x
• x^2+13x+40
• 40+x^2
Вывод: равенство является/не является тождеством.

Условие. Y²+xy-4x-9y+20=0 ;   y=ax+1 ;   x>2

найти все значения а, при которых графики имеют одну общую точку(в нашем случае (ax+1)² + x(ax+1) -4x - 9(ax+1)+20=0 имеет единственное решение).

Подставим у = (ax+1)² в уравнение у²+xy-4x-9y+20=0, получим

Найдем дискриминант квадратного уравнения относительно x

Получим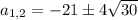

Если подставить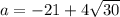 , т.е. имеется квадратное уравнение 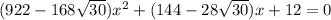, у которого корень

Если подставить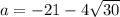 , т.е. имеется квадратное уравнение 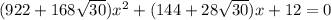, у которого корень

ответ: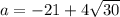

Решить уравнение:      |x+1|-|x-2|+|3x+6|=5.

3|x+2| +|x+1|- |x-2| =5.

 - - -                   +  -  -              + + -                 + + +

(-2) (-1 ) (2)

a) { x < -2 ;  -(3x -6) -(x +1) +(x -2)=5.⇔ { x < -2 ;  x = -14/3.  ⇒ x = -14/3.

б) { -2 ≤ x< - 1 ;  3x+6 -(x+1) +(x -2)=5.⇔ { -2 ≤ x<- 1 ;  x = 2/3.⇒   x ∈∅.

в)  { - 1 ≤ x< 2 ;  3x+6 +(x +1) +(x -2)=5.⇔ {-1 ≤ x< 2 ;  x = 0.  ⇒  x = 0.

д)  { x≥ 2 ;  3x+6 +(x +1) - (x -2)=5.⇔ {1 ≤ x< 2 ;  x = - 4/3.  ⇒  x ∈∅.

ответ:  - 14/3 ; 0 .